题目内容
设函数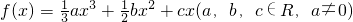 的图象在点(x,f(x))处的切线的斜率为k(x),且函数
的图象在点(x,f(x))处的切线的斜率为k(x),且函数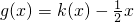 为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式
为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式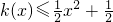 恒成立.
恒成立.
(Ⅰ)求函数k(x)的表达式;
(Ⅱ)求证: (n∈N*).
(n∈N*).
解:(Ⅰ)由已知得:k(x)=f'(x)=ax2+bx+c.…(1分)
由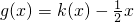 为偶函数,得
为偶函数,得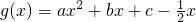 为偶函数,显然有
为偶函数,显然有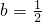 .…(2分)
.…(2分)
又k(-1)=0,所以a-b+c=0,即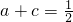 .…(3分)
.…(3分)
又因为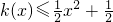 对一切实数x恒成立,
对一切实数x恒成立,
即对一切实数x,不等式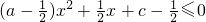 恒成立.…(4分)
恒成立.…(4分)
显然,当 时,不符合题意.…(5分)
时,不符合题意.…(5分)
当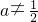 时,应满足
时,应满足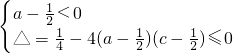 ,
,
注意到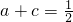 ,解得
,解得 .…(7分) 所以
.…(7分) 所以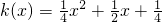 . …(8分)
. …(8分)
(Ⅱ)证明:因为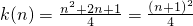 ,所以
,所以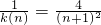 .…(9分)
.…(9分)
要证不等式 成立,
成立,
即证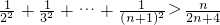 .…(10分)
.…(10分)
因为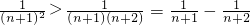 ,…(12分)
,…(12分)
所以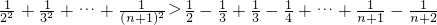 =
=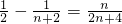 .
.
所以 成立.…(14分)
成立.…(14分)
分析:(Ⅰ)由已知得:k(x)=f'(x),根据g(x)的奇偶性求出b,根据k(-1)=0,求出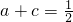 ,再由
,再由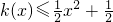 对一切实数x恒成立,解得a、c的值,即得函数k(x)的表达式.
对一切实数x恒成立,解得a、c的值,即得函数k(x)的表达式.
(Ⅱ)根据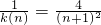 ,即证
,即证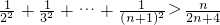 ,把
,把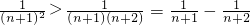 代入要证不等式的左边化简即可证得不等式成立.
代入要证不等式的左边化简即可证得不等式成立.
点评:本题主要考查函数的奇偶性的应用,函数的恒成立问题,利用导数研究曲线在某点的切线斜率,以及用裂项法对数列进行
求和,属于难题.
由
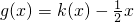 为偶函数,得
为偶函数,得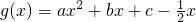 为偶函数,显然有
为偶函数,显然有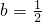 .…(2分)
.…(2分)又k(-1)=0,所以a-b+c=0,即
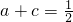 .…(3分)
.…(3分)又因为
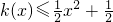 对一切实数x恒成立,
对一切实数x恒成立,即对一切实数x,不等式
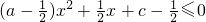 恒成立.…(4分)
恒成立.…(4分)显然,当
 时,不符合题意.…(5分)
时,不符合题意.…(5分)当
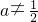 时,应满足
时,应满足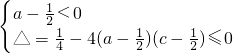 ,
,注意到
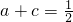 ,解得
,解得 .…(7分) 所以
.…(7分) 所以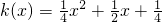 . …(8分)
. …(8分)(Ⅱ)证明:因为
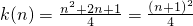 ,所以
,所以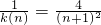 .…(9分)
.…(9分)要证不等式
 成立,
成立,即证
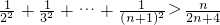 .…(10分)
.…(10分)因为
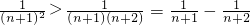 ,…(12分)
,…(12分)所以
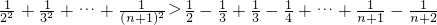 =
=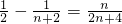 .
.所以
 成立.…(14分)
成立.…(14分)分析:(Ⅰ)由已知得:k(x)=f'(x),根据g(x)的奇偶性求出b,根据k(-1)=0,求出
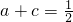 ,再由
,再由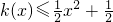 对一切实数x恒成立,解得a、c的值,即得函数k(x)的表达式.
对一切实数x恒成立,解得a、c的值,即得函数k(x)的表达式.(Ⅱ)根据
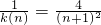 ,即证
,即证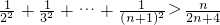 ,把
,把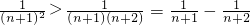 代入要证不等式的左边化简即可证得不等式成立.
代入要证不等式的左边化简即可证得不等式成立.点评:本题主要考查函数的奇偶性的应用,函数的恒成立问题,利用导数研究曲线在某点的切线斜率,以及用裂项法对数列进行
求和,属于难题.

练习册系列答案
相关题目
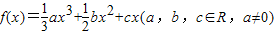 的图象在点(x,f(x))处的切线的斜率为k(x),且函数
的图象在点(x,f(x))处的切线的斜率为k(x),且函数 为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式
为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式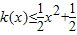 恒成立.
恒成立.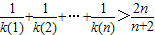 (n∈N*).
(n∈N*). 的图象在点(x,f(x))处的切线的斜率为k(x),且函数
的图象在点(x,f(x))处的切线的斜率为k(x),且函数 为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式
为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式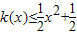 恒成立.
恒成立.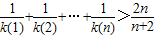 (n∈N*).
(n∈N*).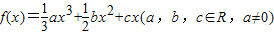 的图象在点(x,f(x))处的切线的斜率为k(x),且函数
的图象在点(x,f(x))处的切线的斜率为k(x),且函数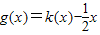 为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式
为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式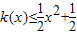 恒成立.
恒成立. (n∈N*).
(n∈N*).