题目内容
(12分)设函数 是奇函数(a,b,c都是整数),且
是奇函数(a,b,c都是整数),且 ,
,
(1)求a,b,c的值;
(2)当x<0, 的单调性如何?用单调性定义证明你的结论。
的单调性如何?用单调性定义证明你的结论。
【答案】
(1)由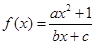 是奇函数,得
是奇函数,得 对定义域内x恒成立,则
对定义域内x恒成立,则
 对定义域内x恒成立,则c=0,
对定义域内x恒成立,则c=0,
(或由定义域关于原点对称得c=0)
又
 又a,b,c是整数,得b=a=1。
又a,b,c是整数,得b=a=1。
(2)由(1)知 ,当x<0,
,当x<0,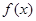 在(-∞,-1)上单调递增,
在(-∞,-1)上单调递增,
在[-1,0)上单调递减,下用定义证明之。
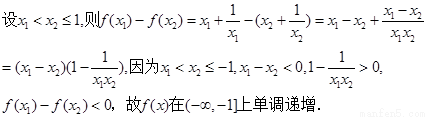
同理,可证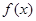 在[-1,0)上单调递减。
在[-1,0)上单调递减。
【解析】略

练习册系列答案
相关题目
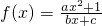 是奇函数(a,b,c都是整数),且f(1)=2,f(2)<3.求a,b,c的值.
是奇函数(a,b,c都是整数),且f(1)=2,f(2)<3.求a,b,c的值.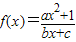 是奇函数(a,b,c都是整数),且f(1)=2,f(2)<3.求a,b,c的值.
是奇函数(a,b,c都是整数),且f(1)=2,f(2)<3.求a,b,c的值.