题目内容
如图,灌溉渠的横截面是等腰梯形,底宽2米,边坡的长为x米、倾角为锐角α.(1)当
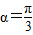 且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;(2)当x=2时,试求灌溉渠的横截面面积的最大值.
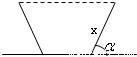
【答案】分析:(1)根据题意可分别表示出梯形的高和上底长,进而可求得横截面的面积的表达式,把 代入S的解析式,利用二次函数的性质判断其单调性,进而推断x=2和x=3时S的值,求得x的最小正整数值.
代入S的解析式,利用二次函数的性质判断其单调性,进而推断x=2和x=3时S的值,求得x的最小正整数值.
(2)把x代入S的解析式中通过对S的函数进行求导,判断S的单调性进而推断出S的最大值.
解答:解:由已知得等腰梯形的高为xsinα,上底长为2+2xcosα,
从而横截面面积S= (2+2+2xcosα)•xsinα=x2sinαcosα+2xsinα.
(2+2+2xcosα)•xsinα=x2sinαcosα+2xsinα.
(1)当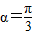 时,面积
时,面积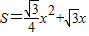 是(0,+∞)上的增函数,
是(0,+∞)上的增函数,
当x=2时,S=3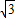 <8;当x=3时,S=
<8;当x=3时,S= .
.
所以,灌溉渠的横截面面积大于8平方米时,x的最小正整数值是3.
(2)当x=2时,S=4sinαcosα+4sinα,S'=4cos2α-4sin2α+4cosα
=4(2cos2α+cosα-1)=4(2cosα-1)•(cosα+1),
由S′=0及α是锐角,
得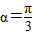 .当0<α<
.当0<α<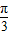 时,S′>0,S是增函数;
时,S′>0,S是增函数;
当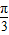 <α<
<α< 时,S′<0,S是减函数.所以,当α=
时,S′<0,S是减函数.所以,当α=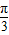 时,S有最大值
时,S有最大值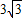 .
.
综上所述,灌溉渠的横截面面积的最大值是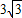 .
.
点评:本题主要考查了在实际问题中建立三角函数模型.考查了考生运用所学知识解决实际问题的能力.
 代入S的解析式,利用二次函数的性质判断其单调性,进而推断x=2和x=3时S的值,求得x的最小正整数值.
代入S的解析式,利用二次函数的性质判断其单调性,进而推断x=2和x=3时S的值,求得x的最小正整数值.(2)把x代入S的解析式中通过对S的函数进行求导,判断S的单调性进而推断出S的最大值.
解答:解:由已知得等腰梯形的高为xsinα,上底长为2+2xcosα,
从而横截面面积S=
 (2+2+2xcosα)•xsinα=x2sinαcosα+2xsinα.
(2+2+2xcosα)•xsinα=x2sinαcosα+2xsinα.(1)当
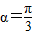 时,面积
时,面积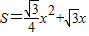 是(0,+∞)上的增函数,
是(0,+∞)上的增函数,当x=2时,S=3
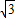 <8;当x=3时,S=
<8;当x=3时,S= .
.所以,灌溉渠的横截面面积大于8平方米时,x的最小正整数值是3.
(2)当x=2时,S=4sinαcosα+4sinα,S'=4cos2α-4sin2α+4cosα
=4(2cos2α+cosα-1)=4(2cosα-1)•(cosα+1),
由S′=0及α是锐角,
得
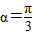 .当0<α<
.当0<α<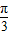 时,S′>0,S是增函数;
时,S′>0,S是增函数;当
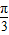 <α<
<α< 时,S′<0,S是减函数.所以,当α=
时,S′<0,S是减函数.所以,当α=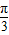 时,S有最大值
时,S有最大值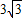 .
.综上所述,灌溉渠的横截面面积的最大值是
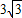 .
.点评:本题主要考查了在实际问题中建立三角函数模型.考查了考生运用所学知识解决实际问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
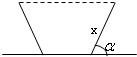 如图,灌溉渠的横截面是等腰梯形,底宽2米,边坡的长为x米、倾角为锐角α.
如图,灌溉渠的横截面是等腰梯形,底宽2米,边坡的长为x米、倾角为锐角α.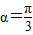 且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;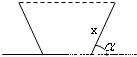
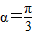 且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;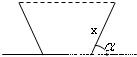
 且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;
且灌溉渠的横截面面积大于8平方米时,求x的最小正整数值;