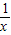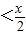题目内容
解下列不等式:
(I)|2x-1|+x+3≤5;
(II)|x+10|-|x-2|≥8.
(I)|2x-1|+x+3≤5;
(II)|x+10|-|x-2|≥8.
分析:(I)将|2x-1|+x+3≤5移项,利用绝对值的意义去掉绝对值符号即可;
(II)利用绝对值的几何意义即可求得|x+10|-|x-2|≥8的解集.
(II)利用绝对值的几何意义即可求得|x+10|-|x-2|≥8的解集.
解答:解:(Ⅰ)∵|2x-1|+x+3≤5,
∴|2x-1|≤-x+2,
∴-(-x+2)≤2x-1≤-x+2.
即
,解之得-1≤x≤1.
所以不等式的解集为{x|-1≤x≤1}.
(Ⅱ)|x+10|和|x-2|分别表示x与-10和2的距离.
当|x+10|-|x-2|=8时,x=0.所以不等式的解集为{x|x≥0}.
∴|2x-1|≤-x+2,
∴-(-x+2)≤2x-1≤-x+2.
即
|
所以不等式的解集为{x|-1≤x≤1}.
(Ⅱ)|x+10|和|x-2|分别表示x与-10和2的距离.
当|x+10|-|x-2|=8时,x=0.所以不等式的解集为{x|x≥0}.
点评:本题考查绝对值不等式的解法,理解绝对值的几何意义是解决问题的关键,属于中档题.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目