题目内容
在平面直角坐标系xOy中,直线l过抛物线y2=4x的焦点F交抛物线于A、B两点.
(1) 若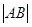 =8,求直线l的斜率
=8,求直线l的斜率
(2)若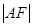 =m,
=m,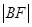 =n.求证
=n.求证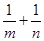 为定值
为定值
(1) 若
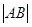 =8,求直线l的斜率
=8,求直线l的斜率(2)若
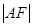 =m,
=m,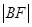 =n.求证
=n.求证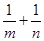 为定值
为定值(1)k=1或-1(2)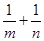 ="1"
="1"
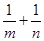 ="1"
="1" 分析:
(1)求出抛物线的焦点坐标,准线方程,设直线l方程为:y=k(x-1),代入y2=4x得[k(x-1)]2=4x,利用韦达定理及抛物线的定义,即可求直线l的斜率
(2)由(1)知,|AF|=m=x1+1,|BF|=n=x2+1,表示出1/m+1/n。利用韦达定理代入化简即可得出结论。
解答:
(1)解:抛物线的焦点坐标为(1,0),准线方程为:x=-1
设直线l方程为:y=k(x-1),代入y2=4x得[k(x-1)]2=4x,即k2x2-(2k2+4)x+k2=0
设A(x1,y1),B(x2,y2),则x1+x2=2k2+4/ k2,x1x2=1
∴2k2+4/ k2=6,∴k2=1
∴k=1或-1。
(2)证明:由(1)知,|AF|=m=x1+1,|BF|=n=x2+1。
∴1/m+1/n=(1/ x1+1)+(1/ x2+1)=(x1+1+x2+1)/[(x1+1)(x2+1)]= (x1+x2+2)/[(x1+x2)+x1x2+1]
∵x1+x2=2k2+4/ k2,x1x2=1
∴(x1+x2+2)/[(x1+x2)+x1x2+1]=1
∴1/m+1/n=1,为定值。
点评:本题重点考查抛物线的标准方程,考查抛物线过焦点的弦,利用抛物线的定义,正确运用韦达定理是解题的关键。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
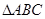 的三个顶点分别为A(0,4),B(-2,6),C(-8,0)
的三个顶点分别为A(0,4),B(-2,6),C(-8,0)
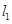 :
: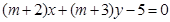 和
和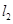 :
: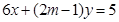 。
。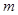 为何值时,有:(1)
为何值时,有:(1) ,
, ,
,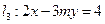 能围成三角形,求m的取值范围.
能围成三角形,求m的取值范围.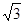 -x与圆x2+y2=2相交于A,B两点,P是优弧AB上任意一点,则∠APB等于( )
-x与圆x2+y2=2相交于A,B两点,P是优弧AB上任意一点,则∠APB等于( ) 
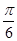


 与
与 垂直,则K
垂直,则K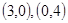 两点的直线方程是( )
两点的直线方程是( )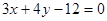



 、
、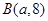 两点的直线与直线
两点的直线与直线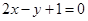 平行,则
平行,则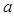 的值为( )
的值为( )
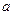 ,第二次出现的点数记为
,第二次出现的点数记为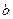 ,设两条直线
,设两条直线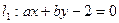 ,
, 平行的概率为
平行的概率为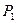 ,相交的概率为
,相交的概率为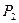 ,则
,则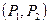 所对应的点在直线
所对应的点在直线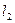 的________方(填“上”或“下”).
的________方(填“上”或“下”).