Question

有4男3女共7位同学从前到后排成一列.

(1)有多少种不同方法？

(2)甲不站在排头，有多少种不同方法？

(3)三名女生互不相邻，有多少种不同方法？

(4)3名女生在队伍中按从前到后从高到矮顺序排列，有多少种不同方法？

(5)3名女生必须站在一起，有多少种不同方法？

 

Answer 1

【答案】

（1）5040 ；（2）4320；（3）1440；（4）840 ；（5）720 。

【解析】

试题分析：（1）7位同学从前到后排成一列，有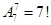=5040种不同方法;

(2) 甲不站在排头，可以将其安排在其它位置，然后再安排其他人员，有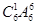=4320种不同方法；

(3)先把四个男孩排成一排有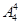种排法，在每一排列中有五个空档（包括两端），再把三个女孩插入空档中有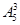种方法，所以共有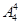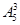=1440种不同方法；

（4）3名女生在队伍中按从前到后从高到矮顺序排列，就是将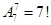中的排法再“去序”，有=840种不同方法

(5)将三名女生“捆绑”视为一个元素，和其他4人进行全排列，3人自身又可调换位置，所以一共有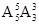＝720种

考点：本题主要考查排列组合应用问题。

点评：中档题，本题较全面地考查了排列组合应用问题，对于“在与不在问题”，常常从特殊元素、特殊位置入手；对于不相邻问题，常用“插空法”（特殊元素后考虑）；对于“相邻问题”常常用“捆绑法”，看成一个元素。