题目内容

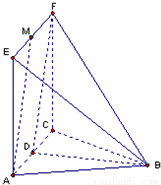
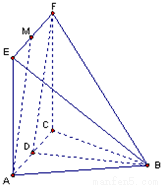
如图,平面EACF⊥平面ABC,△ABC为边长为a的正三角形,四边形ACFE为正方形,点M在线段EF上,点D为AC的中点.
(1)求证:BD⊥平面EACF;
(2)当M在线段EF的什么位置时,AM∥平面BDF,并证明你的结论;
(3)求平面EFB与平面ABC所成的锐二面角的正切值.
分析:(1)证明线面垂直问题一般用线面垂直的判定定理,由题设条件及图形知,可证明两个平面垂直,再证明这条线在一个平面上且垂直于另一个平面.
(2)当点M为线段EF的中点时,AM∥平面BDF,下面要证明当M是中点时,结论成立,根据线面平行的判定定理得到结论.
(3)以D为原点,DA,DB,DM所在直线为x轴,y轴,z轴建立空间直角坐标系D-xyz,写出要用的点的坐标,构造向量,设出平面上的法向量,求出法向量,根据两个向量所成的角的余弦值得到要求的结果.
解答: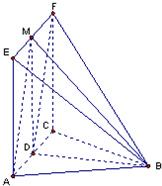
解:(1)证明:∵平面EACF⊥平面ABC,平面EACF∩平面ABC=AC
又∵AB=BC,点D为AC的中点,
∴BD⊥AC∴BD⊥平面EACF.
(2)当点M为线段EF的中点时,AM∥平面BDF.
证明如下:∵M为EF的中点,四边形ACFE为正方形,
∴
MFAD∴四边形AMFC为平行四边形.
∴AM∥DF∵AM?平面BDF,DF?平面BDF
∴AM∥平面BDF.
(3)以D为原点,DA,DB,DM所在直线为x轴,y轴,z轴建立空间直角坐标系D-xyz.
则D(0,0,0),B(0,
a,0),M(0,0,a),E(
,0,a),F(-
,0,a),
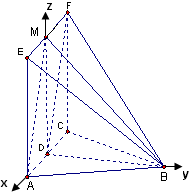
所以
=(,-a,a),=(-,-a,a),由于
⊥平面ABC,所以
可以做为平面ABC的法向量,设
=(x,y,z)是平面EFB的法向量,则由
?得
,所以
x=0,z=y,令y=2,则
=(0,2,),
设平面EFB与平面ABC所成的锐二面角为θ
则
cosθ=||==,
所以
tanθ==.
点评:本题考查空间中直线与平面之间的平行和垂直关系,用空间向量求解夹角,本题解题的关键是建立坐标系,把理论的推导转化成数字的运算,降低了题目的难度.
练习册系列答案
相关题目
 如图,平面EACF⊥平面ABC,△ABC为边长为a的正三角形,四边形ACFE为正方形,点M在线段EF上,点D为AC的中点.
如图,平面EACF⊥平面ABC,△ABC为边长为a的正三角形,四边形ACFE为正方形,点M在线段EF上,点D为AC的中点. 解:(1)证明:∵平面EACF⊥平面ABC,平面EACF∩平面ABC=AC
解:(1)证明:∵平面EACF⊥平面ABC,平面EACF∩平面ABC=AC
 解:(1)证明:∵平面EACF⊥平面ABC,平面EACF∩平面ABC=AC
解:(1)证明:∵平面EACF⊥平面ABC,平面EACF∩平面ABC=AC