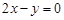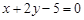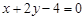题目内容
(12分)已知△ABC中,A(1,1),B(m,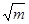 ),C(4,2),1<m<4。
),C(4,2),1<m<4。
求m为何值时,△ABC的面积S最大。
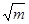 ),C(4,2),1<m<4。
),C(4,2),1<m<4。求m为何值时,△ABC的面积S最大。
当m=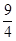 时,△ABC面积最大。
时,△ABC面积最大。
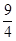 时,△ABC面积最大。
时,△ABC面积最大。本题考查点到直线距离公式的灵活运用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
由|AC|=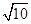 ,知道AC的直线方程为x-2y+2=0,故点B到直线AC的距离是d="|m-3" m+2|
,知道AC的直线方程为x-2y+2=0,故点B到直线AC的距离是d="|m-3" m+2|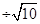 ,由此能推导出当m=9
,由此能推导出当m=9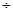 4 时面积最大为Smax=1
4 时面积最大为Smax=1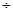 8
8
解:|AC|=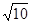 ,直线AC方程为:x-3y+2=0
,直线AC方程为:x-3y+2=0
根据点到直线的距离公式,点B(m,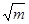 )到直线AC之距d为:
)到直线AC之距d为:
d=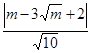
∴S△ABC=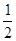 |AC| d=
|AC| d=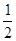 |m-3
|m-3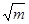 +2|=
+2|=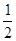 |(
|(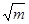 -
- )2-
)2-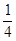 |
|
又∵1<m<4 ∴1<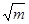 <2
<2
∴当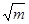 =
= ,即m=
,即m=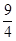 时,S最大。
时,S最大。
故当m=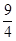 时,△ABC面积最大。
时,△ABC面积最大。
由|AC|=
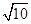 ,知道AC的直线方程为x-2y+2=0,故点B到直线AC的距离是d="|m-3" m+2|
,知道AC的直线方程为x-2y+2=0,故点B到直线AC的距离是d="|m-3" m+2|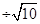 ,由此能推导出当m=9
,由此能推导出当m=9 4 时面积最大为Smax=1
4 时面积最大为Smax=1 8
8 解:|AC|=
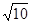 ,直线AC方程为:x-3y+2=0
,直线AC方程为:x-3y+2=0根据点到直线的距离公式,点B(m,
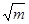 )到直线AC之距d为:
)到直线AC之距d为:d=
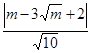
∴S△ABC=
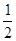 |AC| d=
|AC| d=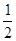 |m-3
|m-3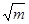 +2|=
+2|=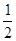 |(
|(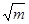 -
- )2-
)2-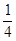 |
|又∵1<m<4 ∴1<
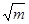 <2
<2∴当
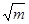 =
= ,即m=
,即m=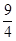 时,S最大。
时,S最大。故当m=
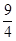 时,△ABC面积最大。
时,△ABC面积最大。
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 过点
过点 ,且与
,且与 轴、
轴、 轴的正半轴分别交于
轴的正半轴分别交于 两点,
两点, 为坐标原点,则三角形
为坐标原点,则三角形 面积的最小值为
面积的最小值为  :
: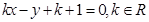 ,则下列结论不正确的是( )
,则下列结论不正确的是( )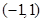
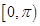
 垂直
垂直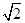
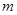 )和Q(
)和Q(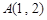 且与直线
且与直线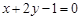 垂直的直线方程是
垂直的直线方程是