题目内容
如图,PD垂直正方形ABCD所在平面,AB=2,E是PB的中点,cos<| DP |
| AE |
| ||
| 3 |
(1)建立适当的空间坐标系,写出点E的坐标;
(2)在平面PAD内求一点F,使EF⊥平面PCB.
分析:(1)以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系,求出
和
的坐标,代入两个向量的夹角公式,解方程求得点E坐标.
(2)由F∈平面PAD,可设F(x,0,z),则
•
=0,且
•
=0,解方程组求得F的坐标.
| AE |
| DP |
(2)由F∈平面PAD,可设F(x,0,z),则
| EF |
| BC |
| EF |
| PC |
解答: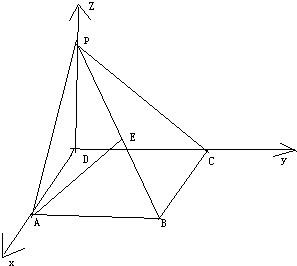 解:(1)以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系,则A(2,0,0),B(2,2,0),C(0,2,0).
解:(1)以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系,则A(2,0,0),B(2,2,0),C(0,2,0).
设P(0,0,2m),则E(1,1,m).
∴
=(-1,1,m),
=(0,0,2m),
∴cos<
,
>=
=
,解得m=1.
∴点E坐标是(1,1,1).
(2)∵F∈平面PAD,∴可设F(x,0,z)?
=(x-1,-1,z-1).
∵EF⊥平面PCB,∴
⊥
?(x-1,-1,z-1)•(2,0,0)=0?x=1.
∵
⊥
,∴(x-1,-1,z-1)•(0,2,-2)=0?z=0.
∴点F的坐标是(1,0,0),即点F是AD的中点.
 解:(1)以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系,则A(2,0,0),B(2,2,0),C(0,2,0).
解:(1)以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系,则A(2,0,0),B(2,2,0),C(0,2,0). 设P(0,0,2m),则E(1,1,m).
∴
| AE |
| DP |
∴cos<
| DP |
| AE |
| 2m2 | ||
|
| ||
| 3 |
∴点E坐标是(1,1,1).
(2)∵F∈平面PAD,∴可设F(x,0,z)?
| EF |
∵EF⊥平面PCB,∴
| EF |
| CB |
∵
| EF |
| PC |
∴点F的坐标是(1,0,0),即点F是AD的中点.
点评:本题考查两个向量的夹角公式,向量和平面垂直的性质,体现了数形结合的数学思想.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
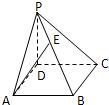 如图,PD垂直正方形ABCD所在的平面,AB=PD=2,动点E在线段PB上,则二面角E-AC-B的取值范围是( )
如图,PD垂直正方形ABCD所在的平面,AB=PD=2,动点E在线段PB上,则二面角E-AC-B的取值范围是( )A、[0,π-arctan
| ||||
B、[0,arctan
| ||||
C、[0,
| ||||
D、[arctan
|
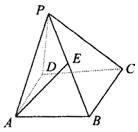
 ,
, >=
>= .
.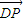 ,
,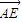 >=
>=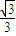 .
.