题目内容
设P是双曲线
上一点，双曲线的一条渐近线方程为3x-2y=O，F1、F2分别是双曲线的左、右焦点，若|PF1|=3，则|PF2|=（ ）A．1或5
B．6
C．7
D．9
【答案】分析：由双曲线的方程、渐近线的方程求出a，由双曲线的定义求出|PF2|．
解答：解：由双曲线的方程、渐近线的方程可得
=
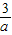，∴a=2．由双曲线的定义可得||PF2|-3|=2 a=4，
∴|PF2|=7，
故选 C．
点评：本题考查双曲线的定义和双曲线的标准方程，以及双曲线的简单性质的应用，由双曲线的方程、渐近线的方程
求出a是解题的关键．
解答：解：由双曲线的方程、渐近线的方程可得
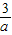=，∴a=2．由双曲线的定义可得||PF2|-3|=2 a=4，∴|PF2|=7，
故选 C．
点评：本题考查双曲线的定义和双曲线的标准方程，以及双曲线的简单性质的应用，由双曲线的方程、渐近线的方程
求出a是解题的关键．
练习册系列答案
相关题目
上一点，双曲线的一条渐近线方程为3x-2y=O，F1、F2
，则
=（
）
上一点，该双曲线的一条渐近线方程是
，
分别是双曲线的左、右焦点，若
，则
等于（
）
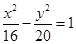上一点，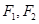
分别是双曲线左右两个焦点，若
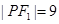，则
=（
）
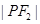上一点，双曲线的一条渐近线方程为3x-2y=O，F1、F2分别是双曲线的左、右焦点，若|PF1|=3，则|PF2|=（ ）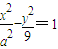
上一点，该双曲线的一条渐近线方程是3x+4y=0，F1，F2分别是双曲线的左、右焦点，若|PF1|=10，则|PF2|等于（ ）