题目内容
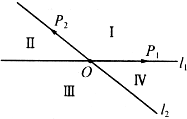 如图,平面内的两条相交直线l1和l2将平面分割成I、II、III、IV四个区域(不包括边界),向量
如图,平面内的两条相交直线l1和l2将平面分割成I、II、III、IV四个区域(不包括边界),向量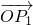 、
、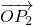 分别为l1和l2的一个方向向量,若
分别为l1和l2的一个方向向量,若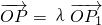
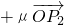 ,且点P落在第II区域,则实数λ、μ满足
,且点P落在第II区域,则实数λ、μ满足
- A.λ>0,μ>0
- B.λ>0,μ<0
- C.λ<0,μ<0
- D.λ<0,μ>0
D
分析:利用两个向量的加法法则和几何意义知,m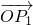 与
与 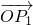 方向相同,n
方向相同,n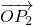 的方向与
的方向与 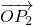 的方向相反.
的方向相反.
解答:∵ =λ•
=λ•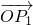 +μ•
+μ•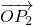 ,且点P落在第II部分,由两个向量的加法法则和几何意义知,
,且点P落在第II部分,由两个向量的加法法则和几何意义知,
λ•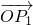 与
与 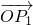 方向相反,
方向相反,
μ•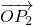 的方向与
的方向与 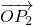 的方向相同,∴λ<0,μ>0.
的方向相同,∴λ<0,μ>0.
故选D.
点评:本题考查两个向量的加法法则及几何意义,一个非零向量乘以一个正实数,方向不变,一个非零向量乘以一个负实数,方向变为原来的相反的方向,属于中档题.
分析:利用两个向量的加法法则和几何意义知,m
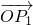 与
与 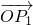 方向相同,n
方向相同,n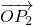 的方向与
的方向与 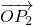 的方向相反.
的方向相反.解答:∵
 =λ•
=λ•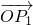 +μ•
+μ•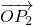 ,且点P落在第II部分,由两个向量的加法法则和几何意义知,
,且点P落在第II部分,由两个向量的加法法则和几何意义知,λ•
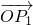 与
与 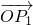 方向相反,
方向相反,μ•
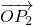 的方向与
的方向与 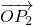 的方向相同,∴λ<0,μ>0.
的方向相同,∴λ<0,μ>0.故选D.
点评:本题考查两个向量的加法法则及几何意义,一个非零向量乘以一个正实数,方向不变,一个非零向量乘以一个负实数,方向变为原来的相反的方向,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目




 是平面PAC内的两条相较直线,所以BD
是平面PAC内的两条相较直线,所以BD 平面PAC,
平面PAC, 平面PAC,所以
平面PAC,所以 .
. 是直线PD和平面PAC所成的角,从而
是直线PD和平面PAC所成的角,从而 .
. 平面PAC,知
平面PAC,知 .在
.在 中,由
中,由 ,所以
,所以 均为等腰直角三角形,从而梯形ABCD的高为
均为等腰直角三角形,从而梯形ABCD的高为 于是梯形ABCD面积
于是梯形ABCD面积 在等腰三角形AOD中,
在等腰三角形AOD中,

 的体积为
的体积为 .
.
 算得体积
算得体积



