题目内容
已知点 ,
,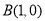 ,直线
,直线 与直线
与直线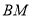 相交于点
相交于点 ,直线
,直线 与直线
与直线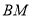 的斜率分别记为
的斜率分别记为 与
与 ,且
,且 .
.
(1)求点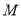 的轨迹
的轨迹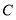 的方程;
的方程;
(2)过定点 作直线
作直线 与曲线
与曲线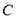 交于
交于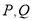 两点,
两点, 的面积是否存在最大值?若存在,求出
的面积是否存在最大值?若存在,求出 面积的最大值;若不存在,请说明理由.
面积的最大值;若不存在,请说明理由.
练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
题目内容
已知点 ,
,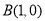 ,直线
,直线 与直线
与直线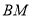 相交于点
相交于点 ,直线
,直线 与直线
与直线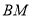 的斜率分别记为
的斜率分别记为 与
与 ,且
,且 .
.
(1)求点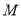 的轨迹
的轨迹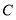 的方程;
的方程;
(2)过定点 作直线
作直线 与曲线
与曲线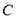 交于
交于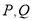 两点,
两点, 的面积是否存在最大值?若存在,求出
的面积是否存在最大值?若存在,求出 面积的最大值;若不存在,请说明理由.
面积的最大值;若不存在,请说明理由.
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案