题目内容
已知向量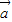 =(1,k),
=(1,k),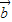 =(2,1),若
=(2,1),若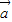 与
与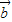 的夹角大小为90°,则实数k的值为( )
的夹角大小为90°,则实数k的值为( )A.-

B.

C.-2
D.2
【答案】分析:根据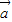 与
与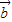 的夹角为90°,即两向量互相垂直,所以
的夹角为90°,即两向量互相垂直,所以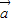 •
•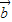 =(1,k)•(2,1)=2+k=0,可得答案.
=(1,k)•(2,1)=2+k=0,可得答案.
解答:解:∵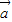 与
与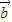 的夹角为90°
的夹角为90°
∴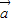 •
•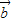 =(1,k)•(2,1)=2+k=0,
=(1,k)•(2,1)=2+k=0,
∴k=-2
故选C.
点评:本题主要考查向量数量积的运算.要明确向量夹角为90°即两向量互相垂直,等价于两向量点乘等于0.
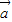 与
与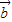 的夹角为90°,即两向量互相垂直,所以
的夹角为90°,即两向量互相垂直,所以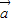 •
•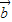 =(1,k)•(2,1)=2+k=0,可得答案.
=(1,k)•(2,1)=2+k=0,可得答案.解答:解:∵
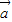 与
与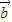 的夹角为90°
的夹角为90°∴
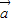 •
•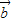 =(1,k)•(2,1)=2+k=0,
=(1,k)•(2,1)=2+k=0,∴k=-2
故选C.
点评:本题主要考查向量数量积的运算.要明确向量夹角为90°即两向量互相垂直,等价于两向量点乘等于0.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知向量
=(1,k),
=(2,1),若
与
的夹角大小为90°,则实数k的值为( )
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
已知向量
=(1,k),
=(2,2),且
+
与
共线,那么
•
的值为( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、1 | B、2 | C、3 | D、4 |