题目内容
由曲线y=|x|与x2+y2=4所围成的图形的最小面积是( )
分析:作出曲线y=|x|与圆x2+y2=4的图象如图所示,可得图中的扇形AOB为所求有最小面积的图形.再由扇形面积公式,结合题中的数据加以计算,可得答案.
解答:解: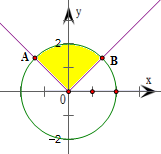 ∵y=|x|=
∵y=|x|=
,
∴作出曲线y=|x|,可得它的图象是第一、二象限的角平分线,如图所示
∵x2+y2=4表示以原点为圆心、半径r=2的圆
∴设曲线y=|x|与圆相交于A、B两点,
可得由劣弧AB与半径OA、OB围成的扇形,即扇形AOB为所求有最小面积的图形.
∵OA⊥OB,
∴扇形AOB的面积S=
×π×22=π.
故选:B
 ∵y=|x|=
∵y=|x|=
|
∴作出曲线y=|x|,可得它的图象是第一、二象限的角平分线,如图所示
∵x2+y2=4表示以原点为圆心、半径r=2的圆
∴设曲线y=|x|与圆相交于A、B两点,
可得由劣弧AB与半径OA、OB围成的扇形,即扇形AOB为所求有最小面积的图形.
∵OA⊥OB,
∴扇形AOB的面积S=
| 1 |
| 4 |
故选:B
点评:本题求曲线围成的图形面积,着重考查了圆的方程、函数图象的作法和扇形面积公式等知识,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目