题目内容
已知数列{an}是等差数列,a5=5,若(6-a1) =a2
=a2 +a3
+a3 ,且A、B、C三点共线(O为该直线外一点);点列(n,bn)在函数
,且A、B、C三点共线(O为该直线外一点);点列(n,bn)在函数 x的反函数的图象上.
x的反函数的图象上.(1)求an和bn;
(2)记数列Cn=anbn+bn(n∈N*),若{Cn}的前n项和为Tn,求使不等式
 成立的最小自然数n的值.
成立的最小自然数n的值.
【答案】分析:(1)利用三点共线的结论,可得6-a1=a2+a3,结合a5=5,求出首项与公差,可求an;利用点列(n,bn)在函数 x的反函数的图象上,可求bn;
x的反函数的图象上,可求bn;
(2)确定数列的通项,利用错位相减法求和,即可求得结论.
解答:解:(1)设数列{an}的公差为d,则
∵(6-a1)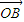 =a2
=a2 +a3
+a3 ,且A、B、C三点共线,
,且A、B、C三点共线,
∴由三点共线的条件,可得6-a1=a2+a3,∴a1+d=2,
∵a5=5,∴a1+4d=5,
∴d=1,a1=1,
∴an=n;
∵点列(n,bn)在函数 x的反函数的图象上
x的反函数的图象上
∴ ;
;
(2)Cn=anbn+bn= ,
,
∴Tn= ,
,
∴ Tn=
Tn=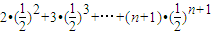
两式相减,可得 Tn=
Tn= =
=
∴Tn=
∴3-Tn=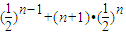
∴ 等价于
等价于
∴n>6
∴使不等式 成立的最小自然数n的值为7.
成立的最小自然数n的值为7.
点评:本题考查数列的通项与求和,考查数列与不等式的联系,确定数列的通项,正确求和是关键.
 x的反函数的图象上,可求bn;
x的反函数的图象上,可求bn;(2)确定数列的通项,利用错位相减法求和,即可求得结论.
解答:解:(1)设数列{an}的公差为d,则
∵(6-a1)
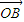 =a2
=a2 +a3
+a3 ,且A、B、C三点共线,
,且A、B、C三点共线,∴由三点共线的条件,可得6-a1=a2+a3,∴a1+d=2,
∵a5=5,∴a1+4d=5,
∴d=1,a1=1,
∴an=n;
∵点列(n,bn)在函数
 x的反函数的图象上
x的反函数的图象上∴
 ;
;(2)Cn=anbn+bn=
 ,
,∴Tn=
 ,
,∴
 Tn=
Tn=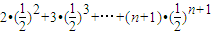
两式相减,可得
 Tn=
Tn= =
=
∴Tn=

∴3-Tn=
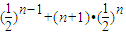
∴
 等价于
等价于
∴n>6
∴使不等式
 成立的最小自然数n的值为7.
成立的最小自然数n的值为7.点评:本题考查数列的通项与求和,考查数列与不等式的联系,确定数列的通项,正确求和是关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目