题目内容

18．若函数f（x）=x3-mx2+mx+3m在（0，1）内有极大值，无极小值，则（　　）
A．m＜0B．m＜3C．0＜m＜3D．m＞3

分析 由题意f′（x）=3x2-2mx+m在（0，1）上先正后负；结合二次函数可得f′（0）=m＞0，f′（1）=3-2m+m＜0；从而解得

解答 解：∵f（x）=x3-mx2+mx+3m，
∴f′（x）=3x2-2mx+m，
又∵f（x）=x3-mx2+mx+3m在（0，1）内有极大值，无极小值；
∴f′（x）=3x2-2mx+m在（0，1）上先正后负；
∴则f′（0）=m＞0，且f′（1）=3-2m+m＜0；
故m＞3；
故选：D．

点评 本题考查了导数的应用及二次函数的性质，属于中档题

练习册系列答案
相关题目
2．△ABC中，∠A=60°，b=1，面积为$\sqrt{2}$，$\frac{a+b+c}{sinA+sinB+sinC}$=$\frac{2}{3}$$\sqrt{35-4\sqrt{6}}$．．
3．已知二次函数f（x）=ax2+bx+c经过点（1，0）和（0，-3），若f（x+2）=f（2-x）
求（1）f（x）的解析式；
（2）当x取何值时f（x+1）＞0．
6．已知f（x）是定义在R上不恒为零的函数，对于任意的x，y∈R，都有f（x•y）=xf（y）+yf（x）成立．数列{an}满足an=f（2n）（n∈N+），且a1=2．
（1）试求数列{an}的通项公式an．
（2）若bn=$\frac{{a}_{n}}{n（n+1）^{2}}$，求数列{bn}的最小项．
13．设a＞0，函数f（x）=$\frac{e^x}{{{x^2}+a}}$．
（1）若a=$\frac{5}{9}$，求函数f（x）的单调区间；
（2）当x=$\frac{1}{2}$时，函数f（x）取得极值，证明：对于任意的${x_1}，{x_2}∈[\frac{1}{2}，\frac{3}{2}]$，|f（x1）-f（x2）|≤$\frac{3-e}{3}\sqrt{e}$．
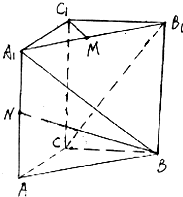3．如图，直三棱柱ABC-A1B1C1，底面△ABC中，CA=CB=2，AB=2$\sqrt{2}$，棱AA1=4，M，N分别是A1B1，AA1的中点．
（1）求$\overrightarrow{{A_1}B}$•$\overrightarrow{{C_1}B}$的值；
（2）求直线BN与平面AB1C所成的角的正弦值．
10．设函数f（x）=x3-3ax2+3（2-a）x，a∈R．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）若y=f（x）的图象与x轴相切于原点，当0＜x2＜x1，f（x1）=f（x2），求证：x1+x2＜8．
7．若角α是第一象限角，则-α，2α，$\frac{α}{3}$分别在哪个区域？
8．求x取何值时，函数y=$\frac{1}{co{s}^{2}x}$-2tanx+2取到最小值时，并求出这个最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网