题目内容
已知复数z1=1-i，|z2|=3，那么|z1-z2|的最大值是______．
根据题意，有|z2|=3，
则z2表示的点为距离原点距离为3的点，
即以原点为圆心，r=3的圆，
那么|z1-z2|的几何意义为圆上的点与点（-1，1）的距离，
设A（-1，-1）
由点与圆的位置关系，分析可得|z1-z2|的最大值是OC+r，
即3+
，
故答案为3+
．
则z2表示的点为距离原点距离为3的点，
即以原点为圆心，r=3的圆，
那么|z1-z2|的几何意义为圆上的点与点（-1，1）的距离，
设A（-1，-1）
由点与圆的位置关系，分析可得|z1-z2|的最大值是OC+r，
即3+
| 2 |
故答案为3+
| 2 |
练习册系列答案
怎样学好牛津英语系列答案
相关题目
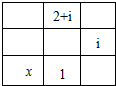
（a,b,c,d∈{－1,1,2}）的所有可能值中，最大的是 .