题目内容
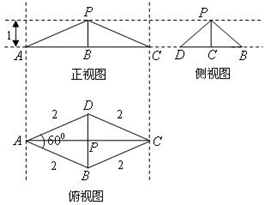 一个四棱锥的三视图如图所示,E为侧棱PC上一动点.
一个四棱锥的三视图如图所示,E为侧棱PC上一动点.(I)画出该四棱锥的直观图,并求它的侧面积
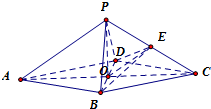
(II)取PC中点E,求证:PA∥面EBD.
分析:(1)根据三视图分析,可得该四棱锥是底面由两个全等正三角形拼成的菱形,顶点P在底面的射影是菱形的中心O,由此不难得出该四棱锥的直观图.利用线面垂直的性质和勾股定理,算出PA=AB=2且PB=
,结合正余弦定理可算出△PAB的面积,进而可得该四棱锥的侧面积.
(2)连接OE,可得OE是△PAC的中位线,得OE∥PA,由线面平行的判定定理,可得出PA∥面EBD.
| 2 |
(2)连接OE,可得OE是△PAC的中位线,得OE∥PA,由线面平行的判定定理,可得出PA∥面EBD.
解答:解:(1)由俯视图可该四棱锥的底面是边长为2且锐角为60°的菱形,由正视图和侧视图,
可得该四棱锥的高恰好是顶点P与底面中心O的连线,且高长等于1
由此可得,它的直观图如下,
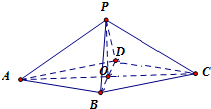
∵△PAB中,PA=
=2,PB=
=
∴cos∠PAB=
=
,得sin∠PAB=
=
由正弦定理,得S△PAB=
×PA×ABsin∠PAB=
同理可得:S△PBC=S△PCD=S△PAD=
∴该四棱锥的侧面积为S=
×4=2
(2)设O为AC、BD的交点,即为底面菱形ABCD的中心,连接OE
∵△PAC中,O、E分别为AC、PC的中点
∴OE∥PA
∵OE?平面EBD,PA?平面EBD
∴PA∥面EBD.
可得该四棱锥的高恰好是顶点P与底面中心O的连线,且高长等于1
由此可得,它的直观图如下,

∵△PAB中,PA=
| PO2+OA2 |
| PO2+BO2 |
| 2 |
∴cos∠PAB=
22+22-(
| ||
| 2×2×2 |
| 3 |
| 4 |
1-(
|
| ||
| 4 |
由正弦定理,得S△PAB=
| 1 |
| 2 |
| ||
| 2 |
同理可得:S△PBC=S△PCD=S△PAD=
| ||
| 2 |

∴该四棱锥的侧面积为S=
| ||
| 2 |
| 7 |
(2)设O为AC、BD的交点,即为底面菱形ABCD的中心,连接OE
∵△PAC中,O、E分别为AC、PC的中点
∴OE∥PA
∵OE?平面EBD,PA?平面EBD
∴PA∥面EBD.
点评:本题给出四棱锥的三视图,求它的直观图并求侧面积,证明了直线与平面平行,着重考查了线面平行的判定定理、三视图的理解和利用正余弦定理求三角表面积等知识,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
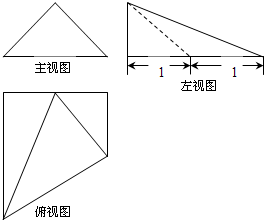 一个四棱锥的三视图如图所示,其中主视图是腰长为1的等腰直角三角形,则这个几何体的体积是( )
一个四棱锥的三视图如图所示,其中主视图是腰长为1的等腰直角三角形,则这个几何体的体积是( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |

 (2012•东城区一模)已知一个四棱锥的三视图如图所示,则该四棱锥的体积是
(2012•东城区一模)已知一个四棱锥的三视图如图所示,则该四棱锥的体积是 一个四棱锥的三视图如图所示,E为侧棱PC上一动点.
一个四棱锥的三视图如图所示,E为侧棱PC上一动点. 已知一个四棱锥的三视图如图所示,其中Rt△PDA≌Rt△PBA,且PD=AD=2,E,F,G分别为PA、PD、CD的中点
已知一个四棱锥的三视图如图所示,其中Rt△PDA≌Rt△PBA,且PD=AD=2,E,F,G分别为PA、PD、CD的中点