题目内容
【题目】如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
(Ⅰ)求证:BE//平面ADE ;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.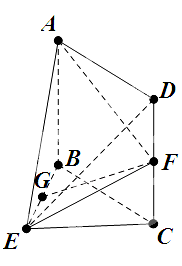
【答案】(I)详见解析;(II)![]() .
.
【解析】
解法一:(I)如图,取AE的中点H,连接HG,HD,又G是BE的中点,所以GH//AB,且GH=![]() AB,又F是CD中点,所以DF=
AB,又F是CD中点,所以DF=![]() CD,由四边形ABCD是平矩形得,AB//CD,且AB=CD,所以GH//DF,且GH=DF,从而四边形HGFD是平行四边形,所以GF//DH,又DH
CD,由四边形ABCD是平矩形得,AB//CD,且AB=CD,所以GH//DF,且GH=DF,从而四边形HGFD是平行四边形,所以GF//DH,又DH![]() 平面ADE,GF
平面ADE,GF![]() 平面ADE,所以GF//平面ADE。
平面ADE,所以GF//平面ADE。
利用其判定定理,或者利用面面平行的性质来证,注意线线平行、线面平行、面面平行的转化;利用坐标法求二面角,主要是空间直角坐标系的建立要恰当,便于用坐标表示相关点,求出半平面法向量夹角后,要观察二面角是锐角还是钝角,正确写出二面角的余弦值。

练习册系列答案
相关题目