题目内容
3位男生和3位女生共6位同学站成一排，若男生甲不站两端，3位女生中有且只有两位女生相邻，则不同的排法的种数是（ ）
| A．360 | B．288 | C．216 | D．96 |
B
解析试题分析：先排三个男生有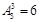
种不同的方法，然后再从3名女生中任取2人“捆”在一起记作A，（A共有C32A22=6种不同排法），剩下一名女生记作B，让A、B插入男生旁边4个位置的两个位置有
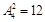，此时共有6×6×12=432种，又男生甲不在两端，其中甲在两端的情况有：2
×6×
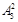=144种不同的排法，∴共有432-144=288种不同排法．故选B
考点：本题考查了排列问题
点评：对于此类问题，解题的关键是看清题目的实质，把实际问题转化为数学问题，解出结果以后再还原为实际问题．
练习册系列答案
相关题目
若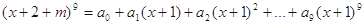
，且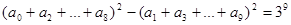
则实数m的值为（ ）
| A．1或-3 | B．-1或3 | C．1 | D．-3 |
如果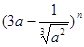
的展开式中各项系数之和为128，则展开式中
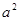的系数是 （ ）
| A．-2835 | B．2835 | C．21 | D．-21 |
设
则
的值是 （ ）
| A．665 | B．729 | C．728 | D．63 |
如果
的展开式中二项式系数之和为128，则展开式中
项的系数是（ ）
| A．7 | B．-7 | C．-21 | D．21 |
设服从二项分布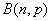
的随机变量
的期望与方差分别是
和
，则
、
的值分别是（ ）．
A． | B． | C． | D． |
设
是
展开式的中间项，若
在区间
上 恒成立，则实数
的取值范围是 ( )
A． | B． | C． | D． |
现有排成一排的7个座位，安排3名同学就座，如果要求剩余的4个座位连在一起，那么不同的坐法总数为（ ）
| A．16 | B．18 | C．24 | D．32 |