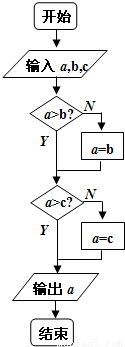
题目内容
sin315°-cos135°+2sin570°的值是( )A.1
B.-1
C.
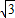
D.-
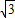
【答案】分析:先把sin315°-cos135°+2sin570°等价转化为sin(270°+45°)-cos(180°-45°)+2sin(360°+210°),再由诱导公式进一步转化为-cos45°+cos45°+2sin210°,然后再用诱导公式能够求出其结果.
解答:解:sin315°-cos135°+2sin570°
=sin(270°+45°)-cos(180°-45°)+2sin(360°+210°)
=-cos45°+cos45°+2sin210°
=2sin(180°+30°)
=-2sin30°
=-1.
故选B.
点评:本题考查诱导公式的简单应用,是基础题.解题时要认真审题,注意三角函数的符号.利用诱导公式解题时的易错点是三角函数的符号出错.
解答:解:sin315°-cos135°+2sin570°
=sin(270°+45°)-cos(180°-45°)+2sin(360°+210°)
=-cos45°+cos45°+2sin210°
=2sin(180°+30°)
=-2sin30°
=-1.
故选B.
点评:本题考查诱导公式的简单应用,是基础题.解题时要认真审题,注意三角函数的符号.利用诱导公式解题时的易错点是三角函数的符号出错.

练习册系列答案
相关题目