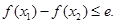题目内容
在实数集R上定义运算: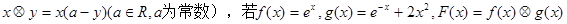
(Ⅰ)求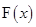 的解析式;
的解析式;
(Ⅱ)若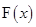 在R上是减函数,求实数a的取值范围;
在R上是减函数,求实数a的取值范围;
(Ⅲ)若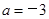 ,在
,在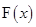 的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不存在,说明理由.
的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不存在,说明理由.
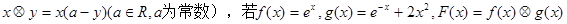
(Ⅰ)求
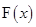 的解析式;
的解析式;(Ⅱ)若
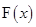 在R上是减函数,求实数a的取值范围;
在R上是减函数,求实数a的取值范围;(Ⅲ)若
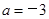 ,在
,在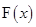 的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不存在,说明理由.
的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不存在,说明理由.(I)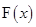
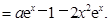 (II)
(II)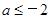 .
.
(III)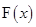 的曲线上不存的两点,使得过这两点的切线点互相垂直.
的曲线上不存的两点,使得过这两点的切线点互相垂直.
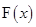
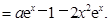 (II)
(II)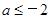 .
. (III)
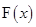 的曲线上不存的两点,使得过这两点的切线点互相垂直.
的曲线上不存的两点,使得过这两点的切线点互相垂直. 试题分析:(I)由新定义计算即得,关键是理解“新运算”的意义;
(II)根据
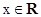 时,
时,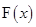 在减函数,得到
在减函数,得到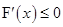 对于
对于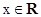 恒成立,
恒成立,即
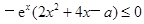 恒成立,得到
恒成立,得到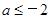 .
.属于常规题目,难度不大,主要是注意应用“转化与化归思想” .
(III)假定
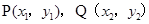 是
是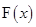 曲线上的任意两点,如果存在互相垂直的切线,则有
曲线上的任意两点,如果存在互相垂直的切线,则有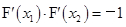 .因此,只需研究
.因此,只需研究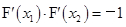 是否成立即可.
是否成立即可.试题解析:(I)由题意,
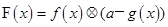 2分
2分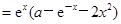
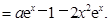 4分
4分(II)∵
 , 6分
, 6分当
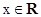 时,
时,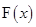 在减函数,
在减函数,∴
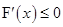 对于
对于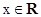 恒成立,即
恒成立,即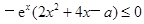 恒成立, 8分
恒成立, 8分∵
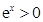 ,
,∴
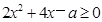 恒成立,
恒成立,∴
 ,
,∴
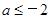 . 9分
. 9分(III)当
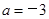 时,
时, ,
,设
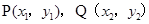 是
是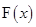 曲线上的任意两点,
曲线上的任意两点,∵
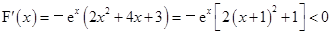 , 11分
, 11分∴
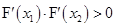 ,
,∴
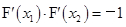 不成立. 12分
不成立. 12分∴
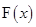 的曲线上不存的两点,使得过这两点的切线点互相垂直. 13分
的曲线上不存的两点,使得过这两点的切线点互相垂直. 13分
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 ,函数
,函数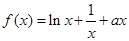 .
.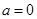 时,求
时,求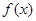 的最小值;
的最小值;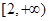 上是单调函数,求
上是单调函数,求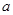 的取值范围.
的取值范围. ,其中a>0.
,其中a>0. 的单调区间;
的单调区间; 是曲线
是曲线 的切线,求实数a的值;
的切线,求实数a的值; ,求
,求 在区间
在区间 上的最大值(其中e为自然对的底数)。
上的最大值(其中e为自然对的底数)。 ,
, .
.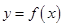 与
与 在它们的交点
在它们的交点 处有相同的切线,求实数
处有相同的切线,求实数 、
、 的值;
的值; 时,若函数
时,若函数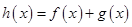 在区间
在区间 内恰有两个零点,求实数
内恰有两个零点,求实数 ,
, 时,求函数
时,求函数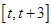 上的最小值.
上的最小值. 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 ),
), (单位:弧度).
(单位:弧度).
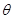 的函数;
的函数; 的前
的前 项和为
项和为 ,已知
,已知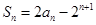 (n∈N*).
(n∈N*).
 ,数列
,数列 的前
的前 项和为
项和为 .利用(2)的结论证明:当n∈N*且n≥2时,
.利用(2)的结论证明:当n∈N*且n≥2时, .
. .
.
 其中
其中 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.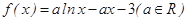 .
.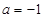 ,求函数
,求函数 的单调区间;
的单调区间;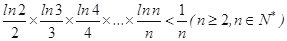
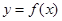 的图象在点
的图象在点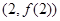 处的切线的倾斜角为
处的切线的倾斜角为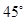 ,对于任意的
,对于任意的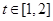 ,函数
,函数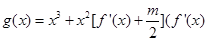 是
是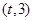 上总不是单调函数,求
上总不是单调函数,求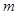 的取值范围。
的取值范围。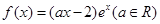 的一个极值点,
的一个极值点,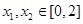 时,证明:
时,证明: