题目内容
(理) 已知点集L={(x,y)|y=| m |
| n |
| m |
| n |
分析:由 y=
•
,
=(x-2b,2),
=(1,b+1),得:y=x+2,由此入手结合题意能够导出an=n(n∈N*),bn=n+2(n∈N*).
| m |
| n |
| m |
| n |
解答:解:由 y=
•
,
=(x-2b, 2),
=(1, 1+b),
得:y=x+2
即L:y=x+2
∵P1为L的轨迹与x=1的交点,
∴P1(1,3)则a1=1,b1=3
∵数列{an}为等差数列,且公差为1,
∴an=n(n∈N*),
代入y=x+2,得:bn=n+2(n∈N*)
故答案为:bn=n+2
| m |
| n |
| m |
| n |
得:y=x+2
即L:y=x+2
∵P1为L的轨迹与x=1的交点,
∴P1(1,3)则a1=1,b1=3
∵数列{an}为等差数列,且公差为1,
∴an=n(n∈N*),
代入y=x+2,得:bn=n+2(n∈N*)
故答案为:bn=n+2
点评:本题考查数列性质的综合运用,具有一定的难度,解题时要注意挖掘隐含条件,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
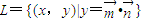 ,其中
,其中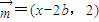 ,
,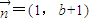 ,点Pn(an,bn)∈L,P1=L∩{(x,y)|x=1},且an+1-an=1,则数列{bn}的通项公式为 .
,点Pn(an,bn)∈L,P1=L∩{(x,y)|x=1},且an+1-an=1,则数列{bn}的通项公式为 .