题目内容
已知双曲线-=1的离心率为e,抛物线x=2py2的焦点为(e,0),则p的值为
A.2 B.1 C. D.
D
解析考点:双曲线的简单性质.
分析:根据双曲线方程可知a和b的值,进而求得c的值,根据e= 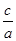 求得e.根据抛物线方程整理成标准方程,根据焦点求得p.
求得e.根据抛物线方程整理成标准方程,根据焦点求得p.
解:依题意得双曲线中a=2,b=2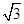
∴c=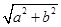 =4
=4
∴e=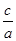 =
=
拋物线方程为y2=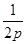 x,故
x,故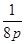 =2,得p=
=2,得p=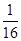 ,
,
故选D.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
若抛物线C:  上一点P到定点A(0,1)的距离为2, 则P到x轴的距离为( )
上一点P到定点A(0,1)的距离为2, 则P到x轴的距离为( )
| A.0 | B.1 | C.2 | D.4 |
已知双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. | C.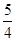 | D. |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A.( ,0) ,0) | B.(0, ) ) | C.( ,0) ,0) | D.(0,-1) |
椭圆的长轴长为10,其焦点到中心的距离为4,则这个椭圆的标准方程为( )
A. | B. |
C. 或 或 | D. 或 或 |
已知椭圆 :
: 的焦点分别为
的焦点分别为 ,如果椭圆上存在点
,如果椭圆上存在点 ,使得
,使得 ·
· ,则椭圆离心率的取值范围是( )
,则椭圆离心率的取值范围是( )
A.( ] ] | B. [ ) ) | C. ( ] ] | D.[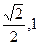 ) ) |
 、
、 分别为双曲线
分别为双曲线 的左、右焦点,若在双曲线右支上存在点
的左、右焦点,若在双曲线右支上存在点 ,满足
,满足 ,且
,且 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为 ( )
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为 ( )



 的离心率为
的离心率为 的焦点坐标为 ( )
的焦点坐标为 ( ) B
B  C
C 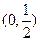 D
D 