题目内容
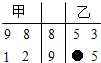 如图的茎叶图是甲、乙两人在4次模拟测试中的成绩,其中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为
如图的茎叶图是甲、乙两人在4次模拟测试中的成绩,其中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为分析:由已知的茎叶图,求出甲乙两人的平均成绩,然后求出乙的平均成绩不小于甲的平均成绩的概率,得到答案.
解答:解:由已知中的茎叶图可得甲的4次综合测评中的成绩分别为88,89,91,92,
则甲的平均成绩:
=90,
设污损数字为x,x∈N,则乙的5次综合测评中的成绩分别为83,83,87,99,90+x,
则乙的平均成绩:
(85+83+95+90+x)=88.25+
,
当x=9,甲的平均数小于或等于乙的平均数,即乙的平均成绩超过甲的平均成绩的概率为
,
当x=8,甲的平均数小于或等于乙的平均数,即乙的平均成绩不小于均甲的平均成绩的概率为
,
当x=7,甲的平均数正好等于乙的平均数,即乙的平均成绩不小于均甲的平均成绩的概率为
.
当0≤x≤6,甲的平均数大于乙的平均数,不满足条件.
故甲的平均成绩不超过乙的平均成绩的概率为
+
+
=
,
故答案为:
.
则甲的平均成绩:
| 88+89+91+92 |
| 4 |
设污损数字为x,x∈N,则乙的5次综合测评中的成绩分别为83,83,87,99,90+x,
则乙的平均成绩:
| 1 |
| 4 |
| x |
| 4 |
当x=9,甲的平均数小于或等于乙的平均数,即乙的平均成绩超过甲的平均成绩的概率为
| 1 |
| 10 |
当x=8,甲的平均数小于或等于乙的平均数,即乙的平均成绩不小于均甲的平均成绩的概率为
| 1 |
| 10 |
当x=7,甲的平均数正好等于乙的平均数,即乙的平均成绩不小于均甲的平均成绩的概率为
| 1 |
| 10 |
当0≤x≤6,甲的平均数大于乙的平均数,不满足条件.
故甲的平均成绩不超过乙的平均成绩的概率为
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 3 |
| 10 |
故答案为:
| 3 |
| 10 |
点评:本题考查的知识点是平均数,茎叶图,古典概型概率计算公式,要求会读图,并且掌握茎叶图的特点:个位数从主干向外越来越大,属简单题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
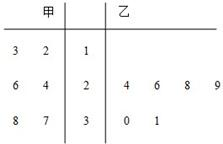 如图所示是某赛季甲、乙两名篮球运动员参加的6场比赛得分的茎叶图,s1,s2分别表示甲、乙两名运动员这个赛季得分的标准差,
如图所示是某赛季甲、乙两名篮球运动员参加的6场比赛得分的茎叶图,s1,s2分别表示甲、乙两名运动员这个赛季得分的标准差,. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是
2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是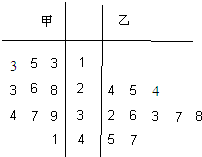 如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则在这几场比赛得分中甲的中位数与乙的众数之和是( )
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则在这几场比赛得分中甲的中位数与乙的众数之和是( )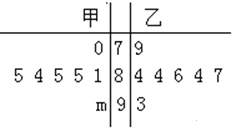 如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲,乙两名歌手得分的平均数分别为a和b,则一定有( )
如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲,乙两名歌手得分的平均数分别为a和b,则一定有( )