题目内容
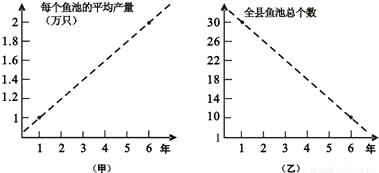
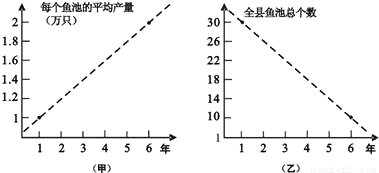
某县畜牧水产局连续6年对该县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图.
甲图调查表明:每个鱼池平均产量直线上升,从第1年1万只鳗鱼上升到第6年2万只.
乙图调查表明:全县鱼池总个数直线下降,由第1年30个减少到第6年10个.
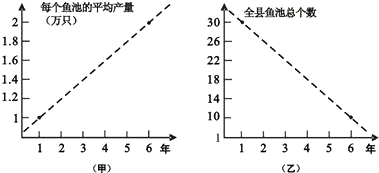
请你根据提供的信息说明:
(Ⅰ)第5年全县鱼池的个数及全县出产的鳗鱼总数;
(Ⅱ)哪一年的规模(即总产量)最大?说明理由.
甲图调查表明:每个鱼池平均产量直线上升,从第1年1万只鳗鱼上升到第6年2万只.
乙图调查表明:全县鱼池总个数直线下降,由第1年30个减少到第6年10个.

请你根据提供的信息说明:
(Ⅰ)第5年全县鱼池的个数及全县出产的鳗鱼总数;
(Ⅱ)哪一年的规模(即总产量)最大?说明理由.
分析:(Ⅰ)甲图象经过(1,1)和(6,2)两点,可以求得其解析式y甲,乙图象经过(1,30)和(6,10)两点,可以求得其解析式y乙,从而计算出第五年鱼池的个数和全县出产鳗鱼总数;
(Ⅱ)设第x年时的规模总出产量为n,x∈N*,应有n=y甲×y乙,经过计算可以得出哪一年的规模(即总产量)最大.
(Ⅱ)设第x年时的规模总出产量为n,x∈N*,应有n=y甲×y乙,经过计算可以得出哪一年的规模(即总产量)最大.
解答:解:(Ⅰ)甲图象经过(1,1)和(6,2)两点,从而求得其解析式为:y甲=
x+
;
乙图象经过(1,30)和(6,10)两点,从而求得其解析式为:y乙=-4x+34;
当x=5时,y甲=
×5+
=
,y乙=-4×5+34=14,∴y甲×y乙=
×14=25.2;
所以,第五年鱼池有14个,全县出产鳗鱼总数为25.2万只;
(Ⅱ)设当第x年时的规模总出产量为n,且x∈N*;那么
n=y甲×y乙=(
x+
)(-4x+34)=-
x2+
x+
=-
(x-
)2+
因此,当x=2时,n有最大值为31.2;即当第2年时,全县鳗鱼养殖业的规模最大.
| 1 |
| 5 |
| 4 |
| 5 |
乙图象经过(1,30)和(6,10)两点,从而求得其解析式为:y乙=-4x+34;
当x=5时,y甲=
| 1 |
| 5 |
| 4 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
所以,第五年鱼池有14个,全县出产鳗鱼总数为25.2万只;
(Ⅱ)设当第x年时的规模总出产量为n,且x∈N*;那么
n=y甲×y乙=(
| 1 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 18 |
| 5 |
| 136 |
| 5 |
| 4 |
| 5 |
| 9 |
| 4 |
| 125 |
| 4 |
因此,当x=2时,n有最大值为31.2;即当第2年时,全县鳗鱼养殖业的规模最大.
点评:本题考查了利用函数图象知识解决实际问题的能力,也考查了运算与处理数据能力;是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
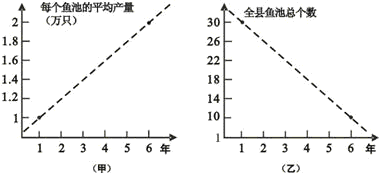 某县畜牧水产局连续6年对该县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图.
某县畜牧水产局连续6年对该县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图.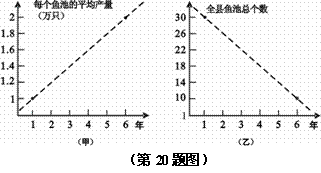 某县畜牧水产局连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
某县畜牧水产局连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图: