题目内容
从集合{x|-5≤x≤16,x∈Z}中任选2个数,作为方程
+
=1中的m和n,
求:(1)可以组成多少个双曲线?
(2)可以组成多少个焦点在x轴上的椭圆?
(3)可以组成多少个在区域B={(x,y)||x|≤2,且|y|≤3}内的椭圆?
| x2 |
| m |
| y2 |
| n |
求:(1)可以组成多少个双曲线?
(2)可以组成多少个焦点在x轴上的椭圆?
(3)可以组成多少个在区域B={(x,y)||x|≤2,且|y|≤3}内的椭圆?
分析:分析集合{x|-5≤x≤16,x∈Z}的元素知:集合中共有16个正数,5个负数
(1)若能构成双曲线,则mn<0,利用乘法原理得出组成多少个双曲线;
(2)若能构成焦点在x轴上的椭圆,则m>n>0,利用乘法原理得出可以组成多少个焦点在x轴上的椭圆;
(3)因为|x|≤2,|y|≤3,得出m≤4,n≤9,因此,可以组成多少个在区域B={(x,y)||x|≤2,且|y|≤3}内的椭圆数.
(1)若能构成双曲线,则mn<0,利用乘法原理得出组成多少个双曲线;
(2)若能构成焦点在x轴上的椭圆,则m>n>0,利用乘法原理得出可以组成多少个焦点在x轴上的椭圆;
(3)因为|x|≤2,|y|≤3,得出m≤4,n≤9,因此,可以组成多少个在区域B={(x,y)||x|≤2,且|y|≤3}内的椭圆数.
解答:解:集合中共有16个正数,5个负数
(1)若能构成双曲线,则mn<0
因此,共有5×16×2=160个 …(5分)
(2)若能构成焦点在x轴上的椭圆,则m>n>0
因此,共有
=120个 …(5分)
(3)因为|x|≤2,|y|≤3,∴m≤4,n≤9,
因此,共有4×8=32个 …(5分)
(1)若能构成双曲线,则mn<0
因此,共有5×16×2=160个 …(5分)
(2)若能构成焦点在x轴上的椭圆,则m>n>0
因此,共有
| 16×15 |
| 2 |
(3)因为|x|≤2,|y|≤3,∴m≤4,n≤9,
因此,共有4×8=32个 …(5分)
点评:本题考查双曲线的标准方程,椭圆的标准方程,椭圆的定义,组合知识,考查学生分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
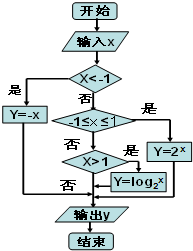 某算法的程序框图如图所示,如果从集合{x|-5≤x≤5,x∈Z}任取一数作为x值输入,则输出的y值大于或等于2的概率为( )
某算法的程序框图如图所示,如果从集合{x|-5≤x≤5,x∈Z}任取一数作为x值输入,则输出的y值大于或等于2的概率为( )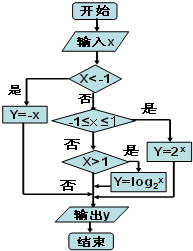 某算法的程序框图如图所示,如果从集合{x|-5≤x≤5,x∈Z}任取一数作为x值输入,则输出的y值大于或等于2的概率为
某算法的程序框图如图所示,如果从集合{x|-5≤x≤5,x∈Z}任取一数作为x值输入,则输出的y值大于或等于2的概率为

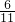






 中的m和n,
中的m和n,