题目内容
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, 为自然对数的底数).
为自然对数的底数).
(1)求 的极值;
的极值;
(2)函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
【答案】
(1)当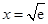 时,
时,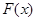 取得极小值0(2)存在隔离直线
取得极小值0(2)存在隔离直线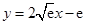
【解析】
试题分析:(1) 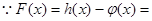
 ,
,
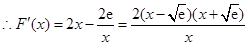 .
.
当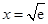 时,
时,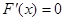 .
.
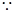 当
当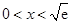 时,
时,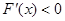 ,此时函数
,此时函数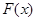 递减;
递减;
当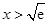 时,
时,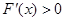 ,此时函数
,此时函数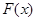 递增;
递增;
∴当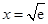 时,
时,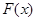 取极小值,其极小值为
取极小值,其极小值为 .
.
(2) :由(1)可知函数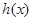 和
和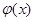 的图象在
的图象在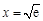 处有公共点,因此若存在
处有公共点,因此若存在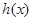 和
和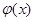 的隔离直线,则该直线过这个公共点.
的隔离直线,则该直线过这个公共点.
设隔离直线的斜率为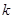 ,则直线方程为
,则直线方程为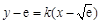 ,即
,即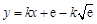 .
.
由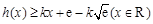 ,可得
,可得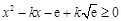 当
当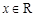 时恒成立.
时恒成立.
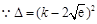 ,
,
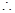 由
由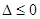 ,得
,得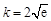 .
.
下面证明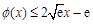 当
当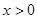 时恒成立.
时恒成立.
令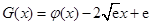
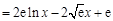 ,则
,则
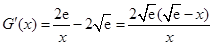 ,
,
当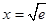 时,
时,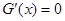 .
.
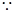 当
当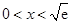 时,
时,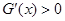 ,此时函数
,此时函数 递增;
递增;
当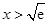 时,
时,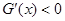 ,此时函数
,此时函数 递减;
递减;
∴当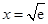 时,
时, 取极大值,其极大值为
取极大值,其极大值为 .
.
从而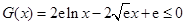 ,即
,即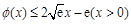 恒成立.
恒成立.
∴函数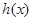 和
和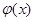 存在唯一的隔离直线
存在唯一的隔离直线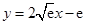 .
.
考点:函数极值最值及不等式恒成立问题
点评:第二问中首先找到两曲线的交点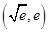 是求解本题的关键,给定信息中满足的不等式恒成立将其转化为求函数最值满足大于等于零或小于等于零,这样即可利用函数导数这一工具来求解
是求解本题的关键,给定信息中满足的不等式恒成立将其转化为求函数最值满足大于等于零或小于等于零,这样即可利用函数导数这一工具来求解

练习册系列答案
相关题目
 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线 为
为 ,
, 为自然对数的底数).
为自然对数的底数). 的极值;
的极值; 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由. 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线
 为
为 ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数). 的极值;
的极值; 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.