题目内容
给定两个命题,p:对任意实数x都有ax2+ax+1>0恒成立;q:关于x的方程x2-x+a=0有实数根;如果p∨q为真命题,p∧q为假命题,求实数a的取值范围。
解:对任意实数x都有ax2+ax+1>0恒成立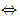 a=0或
a=0或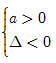
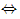 0≤a<4;
0≤a<4;
关于x的方程x2-x+a=0有实数根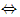 1-4a≥0
1-4a≥0 a≤
a≤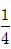 ;
;
如果p正确,且q不正确,有0≤a<4,且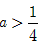 ,
,
∴ <a<4;
<a<4;
如果p不正确,且q正确,有a<0或a≥4,且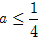 ,
,
∴a<0
所以实数a的取值范围为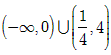 。
。
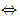 a=0或
a=0或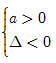
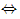 0≤a<4;
0≤a<4;关于x的方程x2-x+a=0有实数根
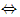 1-4a≥0
1-4a≥0 a≤
a≤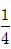 ;
;如果p正确,且q不正确,有0≤a<4,且
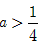 ,
,∴
 <a<4;
<a<4;如果p不正确,且q正确,有a<0或a≥4,且
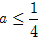 ,
,∴a<0
所以实数a的取值范围为
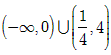 。
。
练习册系列答案
相关题目