题目内容
设m,k为整数,方程mx2-2kx+2=0在区间(0,1)内有两个不同的根,则m+k的最小值为________.
13
分析:设f(x)=mx2-kx+2,要使已知方程在区间(0,1)内两个不同的根,即f(x)的图象在区间(0,1)内与x轴有两个不同的交点,根据图象可得到关于m和k的不等式组,利用线性规划知识可以求解.
解答:设f(x)=mx2-kx+2,由f(0)=2,知f(x)的图象恒过定点(0,2),
因此要使已知方程在区间(0,1)内两个不同的根,即f(x)的图象在区间(0,1)内与x轴有两个不同的交点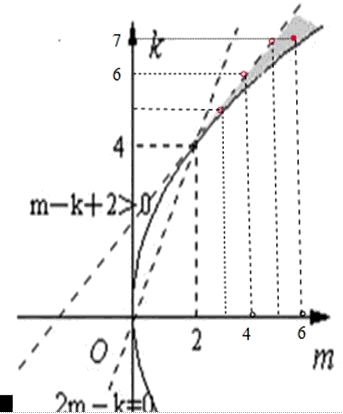
由题意可以得到:必有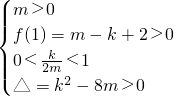 ,即
,即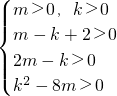
在直角坐标系mok中作出满足不等式平面区域,如图所示,
设z=m+k,则直线m+k-z=0经过图中的阴影中的整点(6,7)时,z=m+k取得最小值,即zmin=13.
所以m+k的最小值为13
故答案为:13.
点评:本题考查二次函数与二次方程之间的联系,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.
分析:设f(x)=mx2-kx+2,要使已知方程在区间(0,1)内两个不同的根,即f(x)的图象在区间(0,1)内与x轴有两个不同的交点,根据图象可得到关于m和k的不等式组,利用线性规划知识可以求解.
解答:设f(x)=mx2-kx+2,由f(0)=2,知f(x)的图象恒过定点(0,2),
因此要使已知方程在区间(0,1)内两个不同的根,即f(x)的图象在区间(0,1)内与x轴有两个不同的交点

由题意可以得到:必有
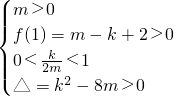 ,即
,即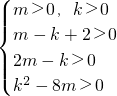
在直角坐标系mok中作出满足不等式平面区域,如图所示,
设z=m+k,则直线m+k-z=0经过图中的阴影中的整点(6,7)时,z=m+k取得最小值,即zmin=13.
所以m+k的最小值为13
故答案为:13.
点评:本题考查二次函数与二次方程之间的联系,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
设m,k为整数,方程mx2-kx+2=0在区间(0,1)内有两个不同的根,则m+k的最小值为( )
| A、-8 | B、8 | C、12 | D、13 |