题目内容
设等差数列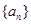 的前
的前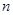 项和为
项和为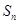 ,若对任意的等差数列
,若对任意的等差数列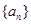 及任意的正整
及任意的正整
数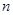 都有不等式设等差数列
都有不等式设等差数列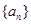 的前
的前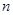 项和为
项和为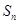 ,若对任意的等差数列
,若对任意的等差数列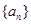 及任意的
及任意的
正整数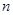 都有不等式
都有不等式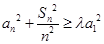 成立,则实数
成立,则实数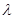 的最大值成立,则实数
的最大值成立,则实数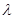 的最大
的最大
值为
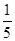
解析试题分析: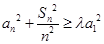
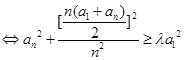
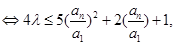
因为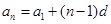 ,所以
,所以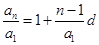 ,令
,令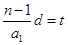 ,则
,则
而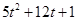 的最小值为
的最小值为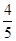 ,所以
,所以
考点:本小题主要考查等差数列的通项公式、前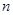 项和的计算和灵活应用,以及不等式
项和的计算和灵活应用,以及不等式
恒成立问题,考查学生转化问题的能力和运算求解能力.
点评:解决此题的关键在于将不等式转化为 解答此类问题时要注意
解答此类问题时要注意
灵活转化.

练习册系列答案
相关题目
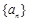 的前
的前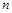 项和为
项和为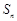 ,
,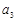 、
、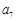 是方程
是方程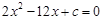 的两根,且
的两根,且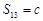 ,则数列
,则数列 .
.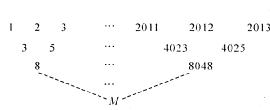
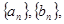
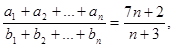 则
则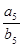 ="___________"
="___________" 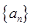 中,
中,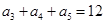 ,那么
,那么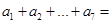
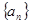 满足
满足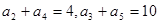 ,则前10项和
,则前10项和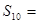
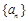 中,如果对任意的
中,如果对任意的 ,都有
,都有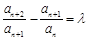 (
(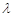 为常数),则称数列
为常数),则称数列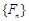 满足
满足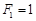 ,
,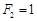 ,
,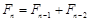 (
(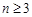 ),则该数列不是比等差数列;②若数列
),则该数列不是比等差数列;②若数列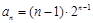 ,则数列
,则数列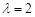 ;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若
;③等比数列一定是比等差数列,等差数列不一定是比等差数列;④若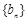 是等比数列,则数列
是等比数列,则数列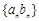 是比等差数列.
是比等差数列.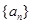 的前
的前 项和为
项和为 ,且
,且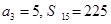 .
.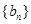 满足:
满足: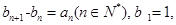 求数列
求数列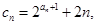 求数列
求数列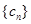 的前
的前