题目内容
已知直线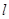 的参数方程为:
的参数方程为: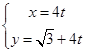 (
(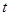 为参数),圆
为参数),圆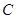 的极坐标方程为
的极坐标方程为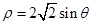 ,那么,直线
,那么,直线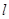 与圆
与圆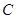 的位置关系是 ( )
的位置关系是 ( )
A.直线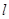 平分圆 平分圆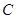 | B.相离 | C.相切 | D.相交 |
D
解析试题分析:先把参数方程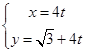 化为
化为 ,再把圆的极坐标方程
,再把圆的极坐标方程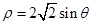 化成
化成 ,再利用圆心到直线的距离
,再利用圆心到直线的距离 .
.
考点:1.参数方程;2.极坐标.

练习册系列答案
相关题目
设曲线 的参数方程为
的参数方程为 (
(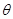 为参数),直线
为参数),直线 的方程为
的方程为 ,则曲线
,则曲线 上到直线
上到直线 距离为
距离为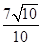 的点的个数为
的点的个数为


| A.1 | B.2 | C.3 | D.4 |
直线 被圆
被圆 截得的弦长为( )
截得的弦长为( )
A. | B. | C. | D. |
若直线L的参数方程为 为参数),则直线L的倾斜角的余弦值为( )
为参数),则直线L的倾斜角的余弦值为( )
A. | B.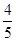 | C. | D. |
设曲线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 的方程为
的方程为 ,则曲线
,则曲线 上到直线
上到直线 距离为
距离为 的点的个数为( )
的点的个数为( )
| A.1 | B.2 | C.3 | D.4 |
在极坐标系下,已知圆C的方程为r=2cosθ,则下列各点中,在圆C上的是( )
A.(1,- ) ) | B.(1, ) ) |
C.(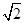 , , ) ) | D.(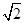 , ,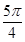 ) ) |
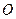 的直径
的直径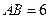 ,
,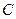 为圆周上一点,
为圆周上一点, ,过
,过 ,过
,过 作
作 ,垂足为
,垂足为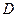 ,求∠DAC
,求∠DAC
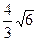 ,AC边上的中线BD=
,AC边上的中线BD=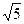 ,cosB=
,cosB=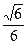 ,如图所示,
,如图所示,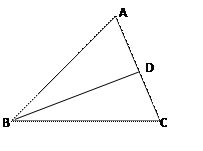 求:sinA。
求:sinA。 (s为参数)和直线l2:
(s为参数)和直线l2: (t为参数)平行,则常数a的值为________.
(t为参数)平行,则常数a的值为________.