题目内容
若抛物线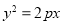 的焦点坐标为
的焦点坐标为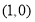 ,则准线方程为 .
,则准线方程为 .
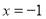
【解析】
试题分析:由抛物线的方程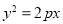 可知抛物线的焦点为
可知抛物线的焦点为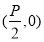 ,准线为
,准线为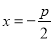 ,而焦点的坐标为
,而焦点的坐标为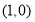 ,所以
,所以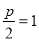 , 所以抛物线的准线方程为
, 所以抛物线的准线方程为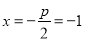 .
.
考点:抛物线的标准方程及其几何性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
若抛物线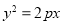 的焦点坐标为
的焦点坐标为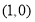 ,则准线方程为 .
,则准线方程为 .
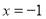
【解析】
试题分析:由抛物线的方程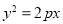 可知抛物线的焦点为
可知抛物线的焦点为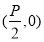 ,准线为
,准线为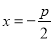 ,而焦点的坐标为
,而焦点的坐标为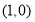 ,所以
,所以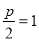 , 所以抛物线的准线方程为
, 所以抛物线的准线方程为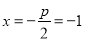 .
.
考点:抛物线的标准方程及其几何性质.

 阅读快车系列答案
阅读快车系列答案