题目内容
设集合P={x1,x2,x3,…,x10},则从集合P的全部子集中任取一个,取到的含有3个元素的子集的概率是
.
| 15 |
| 128 |
| 15 |
| 128 |
分析:由题意可得集合P={x1,x2,x3,…,x10}子集共有210=1024个,从集合P的全部子集中任取一个,取到的含有3个元素的子集的结果有C103=120种,由等可能事件的概率公式可求
解答:解:由题意可得集合P={x1,x2,x3,…,x10}子集共有210=1024个
记“从集合P的全部子集中任取一个,取到的含有3个元素的子集”为事件A,则A包含的结果有C103=120种
由等可能事件的概率公式可得,P(A)=
=
故答案为:
记“从集合P的全部子集中任取一个,取到的含有3个元素的子集”为事件A,则A包含的结果有C103=120种
由等可能事件的概率公式可得,P(A)=
| 120 |
| 1024 |
| 15 |
| 128 |
故答案为:
| 15 |
| 128 |
点评:本题主要考查了等可能事件的概率的求解,解题的关键是利用集合的性质:一个含有n个元素 集合的子集个数为2n个,及利用排列组合求解基本事件的个数,属于基础试题

练习册系列答案
相关题目
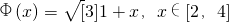 ,证明:Φ(x)∈A;
,证明:Φ(x)∈A;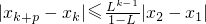 成立.
成立.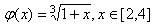 ,证明:φ(x)∈A;
,证明:φ(x)∈A;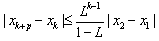 。
。 。
。 ,证明:Φ(x)∈A;
,证明:Φ(x)∈A; 成立.
成立. ,证明:Φ(x)∈A;
,证明:Φ(x)∈A; 成立.
成立.