题目内容
（不等式选讲）若实数x，y，z满足x2+y2+z2=9，则x+2y+3z的最大值是 ．
分析：由柯西不等式可得：（x2+y2+z2）×（12+22+32）≥（x+2y+3z）2，结合已知x2+y2+z2=9，可求x+2y+3z的最大值．
解答：解：由柯西不等式可得：（x2+y2+z2）×（12+22+32）≥（x+2y+3z）2
已知x2+y2+z2=9，
∴（x+2y+3z）2≤9×14，
∴x+2y+3z的最大值是3
．
故答案为：3
．
已知x2+y2+z2=9，
∴（x+2y+3z）2≤9×14，
∴x+2y+3z的最大值是3
| 14 |
故答案为：3
| 14 |
点评：本题考查柯西不等式，构造柯西不等式（x2+y2+z2）×（12+22+32）≥（x+2y+3z）2是关键．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
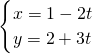（t为参数）与直线4x+ky=1垂直，则常数k=________．