题目内容
设n为偶数,则8n+Cn18n-1+Cn28n-2+…+Cnn-18被10整除的余数是
- A.0
- B.1
- C.2
- D.-1
A
分析:由组合数的性质知8n+Cn18n-1+Cn28n-2+…+Cnn-18=99-1=(10-1)9-1,按照二项式定理展开即可求出结果.
解答:由组合数的性质知8n+Cn18n-1+Cn28n-2+…+Cnn-18=9n-1
=(10-1)n-1=10n+Cn110n-1(-1)+Cn210n-2(-1)2+…+Cnn-1101(-1)n-1+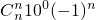 -1
-1
n为偶数,按照二项式定理展开,前边的项都能被10整除,最后一项为1,故和值除以10的余数为 0.
故选A.
点评:本题考查组合数的性质、二项式定理的应用:整除问题,考查利用所学知识分析问题、解决问题的能力.
分析:由组合数的性质知8n+Cn18n-1+Cn28n-2+…+Cnn-18=99-1=(10-1)9-1,按照二项式定理展开即可求出结果.
解答:由组合数的性质知8n+Cn18n-1+Cn28n-2+…+Cnn-18=9n-1
=(10-1)n-1=10n+Cn110n-1(-1)+Cn210n-2(-1)2+…+Cnn-1101(-1)n-1+
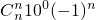 -1
-1n为偶数,按照二项式定理展开,前边的项都能被10整除,最后一项为1,故和值除以10的余数为 0.
故选A.
点评:本题考查组合数的性质、二项式定理的应用:整除问题,考查利用所学知识分析问题、解决问题的能力.

练习册系列答案
相关题目