题目内容
已知函数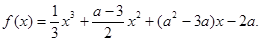
(I)如果对任意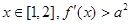 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(II)设函数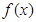 的两个极值点分别为
的两个极值点分别为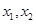 判断下列三个代数式:
判断下列三个代数式:
①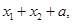 ②
②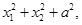 ③
③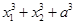 中有几个为定值?并且是定值请求出;
中有几个为定值?并且是定值请求出;
若不是定值,请把不是定值的表示为函数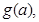 并求出
并求出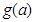 的最小值.
的最小值.
【答案】
(I)a<-2. (II)最小值为15,判断见解析。
【解析】(I)本小题的实质就是求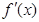 在
在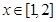 上的最小值,令其最小值大于
上的最小值,令其最小值大于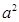 解关于a的不等式求出a的取值范围.
解关于a的不等式求出a的取值范围.
(II)由题意可知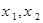 恰为方程
恰为方程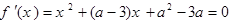 的两根,从而可得到
的两根,从而可得到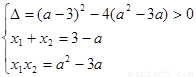 解得
解得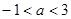 ,进而可得
,进而可得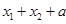 =3为定值;
=3为定值;
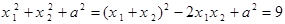 为定值;
为定值;
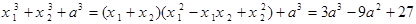 不是定值;
不是定值;
然后再利用导数求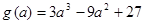 (
(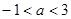 )的最小值即可.
)的最小值即可.
解:(1)由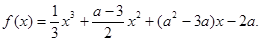
得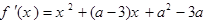 ,对任意
,对任意 恒成立,
恒成立,
即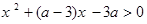 ,
,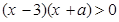 对任意
对任意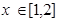 恒成立,
恒成立,
又x-3<0恒成立,所以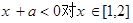 恒成立,所以
恒成立,所以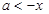 恒成立,
恒成立,
所以a<-2. ………………4分
(2)依题意知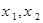 恰为方程
恰为方程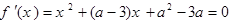 的两根,
的两根,
所以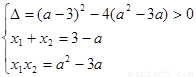 解得
解得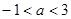 ………………5分
………………5分
所以①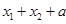 =3为定值, ………6分
=3为定值, ………6分
②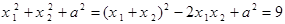 为定值,………………7分
为定值,………………7分
③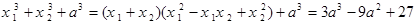 不是定值
不是定值
即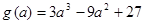 (
(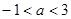 )所以
)所以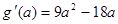 ,
,
当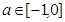 时,
时,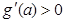 ,
,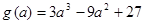 在
在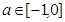 是增函数,
是增函数,
当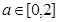 时,
时,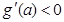 ,
,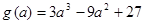 在
在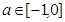 是减函数,
是减函数,
当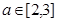 时,
时,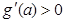 ,
,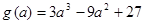 在
在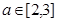 是增函数,
是增函数,
所以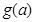 在
在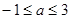 的最小值需要比较
的最小值需要比较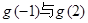 ,因为
,因为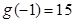 ;
;
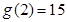 所以
所以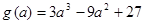 (
( )的最小值为15(a=2时取到)12分
)的最小值为15(a=2时取到)12分

练习册系列答案
相关题目
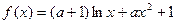
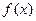 的单调性;
的单调性;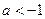 .如果对任意
.如果对任意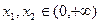 ,
,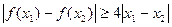 ,求
,求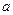 的取值范围。
的取值范围。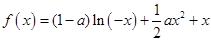
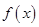 在
在 处的切线过(0,1)点,求
处的切线过(0,1)点,求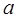 的值;
的值;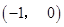 为增函数,求实数
为增函数,求实数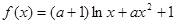
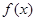 的单调性;
的单调性;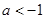 .如果对任意
.如果对任意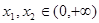 ,
,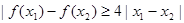 ,求
,求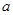 的取值范围。
的取值范围。