题目内容
已知二次函数
，关于实数
的不等式
的解集为
．
（1）当
时，解关于
的不等式：
；
（2）是否存在实数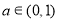
，使得关于
的函数
（
）的最小值为
？若存在，求实数
的值；若不存在，说明理由．
练习册系列答案
同步练习强化拓展系列答案
相关题目
同步练习强化拓展系列答案题目内容
已知二次函数，关于实数的不等式的解集为．
（1）当时，解关于的不等式：；
（2）是否存在实数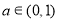，使得关于的函数（）的最小值为？若存在，求实数的值；若不存在，说明理由．
同步练习强化拓展系列答案
.
,解不等式 
;
恒成立，求实数
的取值范围.
的前
项和
，且
，则
．
，
是虚数单位，则复数
的虚部为 ．
若
，则实数
的取值范围是 ．
（
且
）恒过定点 ．
的外接球为球
，球
，且
都是边长为
的等边三角形，则三棱锥
B．
C.
D．
的底面四边形
为平行四边形，其中
，且
相交于
.
平面
;
,点
是
中点求三棱锥
的体积.