题目内容
7. 如图正方形ABCD的边长为ABCD的边长为$2\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,$FO=\sqrt{3},且FO⊥$平面ABCD.
如图正方形ABCD的边长为ABCD的边长为$2\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,$FO=\sqrt{3},且FO⊥$平面ABCD.(I)求证:AE∥平面BCF;
(Ⅱ)若$FO=\sqrt{3}$,求证CF⊥平面AEF.
分析 (I)利用正方形,平行四边形的性质可得AD∥BC,DE∥BF,可证平面ADE∥平面BCF,即可证明AE∥平面BCF…5分
(Ⅱ)由已知可证AC2=AF2+CF2,由勾股定理可得CF⊥AF,又FO⊥平面ABCD,可得FO⊥BD,又AC⊥BD,即可证明BD⊥平面AFC,结合EF∥BD,即可证明EF⊥CF,从而可证CF⊥平面AEF.
解答  证明:(I)∵四边形ABCD为正方形,四边形BDEF是平行四边形,
证明:(I)∵四边形ABCD为正方形,四边形BDEF是平行四边形,
∴AD∥BC,DE∥BF,
∵AD∩DE=D,BC∩BF=B,
∴平面ADE∥平面BCF,
又∵AE?平面ADE,
∴AE∥平面BCF…5分
(Ⅱ)∵正方形ABCD边长为2$\sqrt{2}$,
∴对角线AC=4,
又∵O为GC中点,
∴AO=3,OC=1
又∵FO⊥平面ABCD,且FO=$\sqrt{3}$,
∴AF2=AO2+OF2=9+3=12,CF2=OC2+OF2=1+3=4,
又AC2=16,
∴AC2=AF2+CF2,
∴CF⊥AF,
又FO⊥平面ABCD,BD?平面ABCD,
∴FO⊥BD
又∵AC⊥BD
∴BD⊥平面AFC,
又∵EF∥BD,
∴EF⊥平面AFC
∴EF⊥CF,
又EF∩AF=F
∴CF⊥平面AEF…12分
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
12.下列各组函数f(x)与g(x)的图象相同的是( )
| A. | f(x)=x,g(x)=($\sqrt{x}$)2 | B. | $f(x)=\frac{{{x^2}-4}}{x-2}$与g(x)=x+2 | ||
| C. | f(x)=1,g(x)=x0 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,(x≥0)}\\{-x,(x<0)}\end{array}\right.$ |
16.已知命题p:x2-x-2>0,q:|x|<a,若¬p是q的必要而不充分条件,则实数a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a<2 | D. | a≤2 |
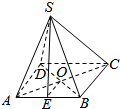 如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.
如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小. 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.