题目内容
假设位于正四面体ABCD顶点处的一只小虫,沿着正四面体的棱随机地在顶点间爬行,记小虫沿棱从一个顶点爬到另一个顶点为一次爬行,小虫第一次爬行由A等可能地爬向B、C、D中的任意一点,每二次爬行又由其所在顶点等可能地爬向其它三点中的任意一点,如此一直爬下去,记第n(n∈N*)次爬行小虫位于顶点A处的概率为pn.
(1)求p1,p2,p3的值,并写出pn的表达式(不要求证明);
(2)设Sn=p1
+p2
+p3
+…+pn
(n∈N*),试求Sn(用含n的式子表示).
(1)求p1,p2,p3的值,并写出pn的表达式(不要求证明);
(2)设Sn=p1
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
分析:(1)根据小虫沿棱从一个顶点爬到另一个顶点为一次爬行,小虫第一次爬行由A等可能地爬向B、C、D中的任意一点,每二次爬行又由其所在顶点等可能地爬向其它三点中的任意一点,可求出p1,p2,p3的值,从而可猜想出pn的表达式;
(2)根据pn的表达式,利用分组求和法以及二项式定理的逆用、二项式系数的和从而可求出所求.
(2)根据pn的表达式,利用分组求和法以及二项式定理的逆用、二项式系数的和从而可求出所求.
解答:解:(1)p1=0,p2=
,p3=
(1-p2)=
,p4=
(1-p3)=
猜想:pn=
[1-(-
)n-1]
(2)Sn=p1
+p2
+p3
+…+pn
(n∈N*)
=
(
+
+…+
)+
[
(-
)1+
(-
)2+…
(-
)n]
=
(
+
+
+…+
)+
[
(-
)0+
(-
)1+
(-
)2+…
(-
)n]
=
•2n+
(1-
)n-1
=2n-2+
(
)n-1-1
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
| 7 |
| 27 |
猜想:pn=
| 1 |
| 4 |
| 1 |
| 3 |
(2)Sn=p1
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
=
| 1 |
| 4 |
| C | 1 n |
| C | 2 n |
| C | n n |
| 3 |
| 4 |
| C | 1 n |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 3 |
| C | n n |
| 1 |
| 3 |
=
| 1 |
| 4 |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| 3 |
| 4 |
| C | 0 n |
| 1 |
| 3 |
| C | 1 n |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 3 |
| C | n n |
| 1 |
| 3 |
=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
=2n-2+
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题主要考查了等比数列的通项,以及二项式系数的性质,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
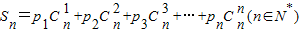 ,试求Sn(用含n的式子表示).
,试求Sn(用含n的式子表示).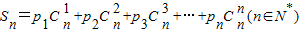 ,试求Sn(用含n的式子表示).
,试求Sn(用含n的式子表示).