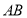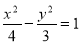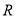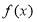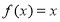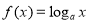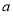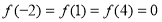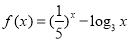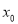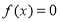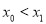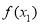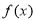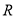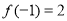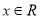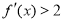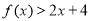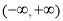题目内容
对于函数 ,若在定义域内存在实数
,若在定义域内存在实数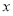 ,满足
,满足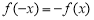 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知函数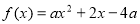
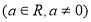 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若 为定义域
为定义域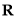 上的“局部奇函数”,求实数m的取值范围.
上的“局部奇函数”,求实数m的取值范围.
(1)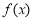 为“局部奇函数”; (2)
为“局部奇函数”; (2)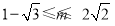
【解析】
试题分析:(1)若方程 有解,则说明
有解,则说明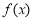 是“局部奇函数”,否则,则说明
是“局部奇函数”,否则,则说明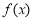 不是“局部奇函数”。 (2)当
不是“局部奇函数”。 (2)当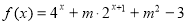 时,
时,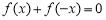 可化为
可化为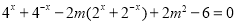 ,用整体思想将
,用整体思想将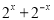 视为整体用
视为整体用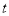 表示。将上式转化为
表示。将上式转化为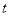 的一元二次函数。根据题意可知此二次函数在其定义域上有解。
的一元二次函数。根据题意可知此二次函数在其定义域上有解。
试题解析:【解析】
(1)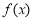 为“局部奇函数”等价于关于x的方程
为“局部奇函数”等价于关于x的方程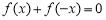 有解.
有解.
当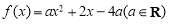 时,
时,
由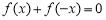 得
得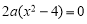
解得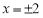 ,
,
所以方程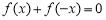 有解,因此
有解,因此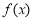 为“局部奇函数”. 4分
为“局部奇函数”. 4分
(2)当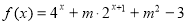 时,
时,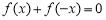 可化为
可化为
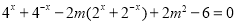 .
.
令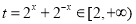 , 则
, 则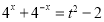 , 6分
, 6分
从而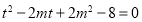 在
在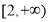 有解即可保证
有解即可保证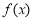 为“局部奇函数”. 8分
为“局部奇函数”. 8分
令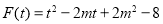 ,
,
1° 当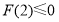 ,
,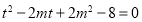 在
在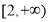 有解,
有解,
由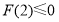 ,即
,即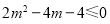 ,解得
,解得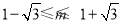 ; 10分
; 10分
2° 当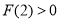 时,
时,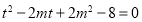 在
在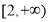 有解等价于
有解等价于
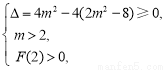 解得
解得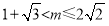 . 13分
. 13分
(说明:也可转化为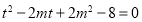 的大根大于等于2求解)
的大根大于等于2求解)
综上,所求实数m的取值范围为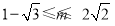 . 14分
. 14分
考点:1新概念问题;2指数函数的值域;3二次函数。

练习册系列答案
相关题目