题目内容
(文)(本题满分12分)、已知直线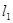 :3x+4y﹣5=0,圆O:x2+y2=4.
:3x+4y﹣5=0,圆O:x2+y2=4.
(1)求直线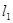 被圆O所截得的弦长;
被圆O所截得的弦长;
(2)如果过点(﹣1,2)的直线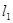 与
与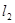 垂直,
垂直,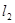 与圆心在直线x﹣2y=0上的圆M相切,圆M被直线
与圆心在直线x﹣2y=0上的圆M相切,圆M被直线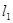 分成两段圆弧,其弧长比为2:1,求圆M的方程.
分成两段圆弧,其弧长比为2:1,求圆M的方程.
【答案】
(1)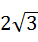 (2) x2+y2=4
(2) x2+y2=4
【解析】
试题分析:解:(1)由题意得:圆心到直线l1:3x+4y﹣5=0的距离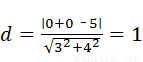 ,由垂径定理得弦长为
,由垂径定理得弦长为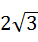 。
。
(2)直线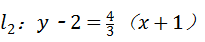
设圆心M为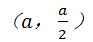 圆心M到直线l1的距离为r,即圆的半径,由题意可得,圆心M到直线l2的距离为
圆心M到直线l1的距离为r,即圆的半径,由题意可得,圆心M到直线l2的距离为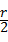 ,所以有:
,所以有: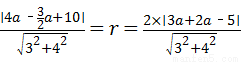
解得: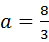 ,所以圆心为
,所以圆心为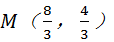 ,
,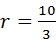 ,所以所求圆方程为:
,所以所求圆方程为: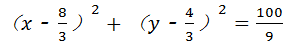
或a=0,即圆方程为:x2+y2=4
考点:本试题考查了直线与圆的位置关系,以及圆的方程的求解。
点评:解决直线与圆相交的弦长问题。一般可以运用几何法来结合勾股定理来求解得到。也可以通过代数的方法联立方程组,结合韦达定理来求解。是一个重要的知识点,需要熟练的掌握。属于中档题。

练习册系列答案
相关题目
 和
和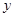 轴相切,圆心在直线
轴相切,圆心在直线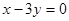 上,且被直线
上,且被直线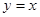 截得的弦长为
截得的弦长为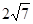
 ,求圆
,求圆 :3x+4y﹣5=0,圆O:x2+y2=4.
:3x+4y﹣5=0,圆O:x2+y2=4. 垂直,
垂直,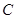 和
和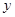 轴相切,圆心在直线
轴相切,圆心在直线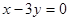 上,且被直线
上,且被直线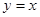 截得的弦长为
截得的弦长为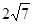
 ,求圆
,求圆