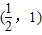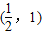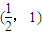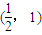题目内容
抛物线y=4x2上一点到直线y=4x-5的距离最短,则该点的坐标是( )
| A、(1,2) | ||
| B、(0,0) | ||
C、(
| ||
| D、(1,4) |
分析:根据题意,直线y=4x-5必然与抛物线y=4x2相离,抛物线上的点到直线的最短距离就是与直线y=4x-5平行的抛物线的切线的切点.
解答:解:y'=8x,由8x=4得x=
,
故抛物线的斜率为4的切线的切点坐标是(
,1),
该点到直线y=4x-5的距离是最短.
故选C.
| 1 |
| 2 |
故抛物线的斜率为4的切线的切点坐标是(
| 1 |
| 2 |
该点到直线y=4x-5的距离是最短.
故选C.
点评:主要考查了导数及其应用,本题以数形结合思想为指导命制,通过形的分析把问题转化为求抛物线的斜率为4的切线的切点坐标.本题也可以直接根据点到直线的距离公式求解,即抛物线上的点到直线y=4x-5的距离是d=
=
=
,显然这个函数当x=
时取得最小值,此时y=1.
| |4x-y-5| | ||
|
| |4x-4x2-5| | ||
|
4(x-
| ||
|
| 1 |
| 2 |

练习册系列答案
相关题目