题目内容
设p:函数y=loga(x+1)(a＞0且a≠1)在(0,+∞)上单调递减; q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p∧q为假，p∨q为真，求实数a的取值范围.
【答案】
≤a＜1或a＞
.
【解析】
试题分析：∵函数y=loga(x+1)在(0,+∞)上单调递减,
∴0＜a＜1，即p:0＜a＜1, 2分
∵曲线y=x2+(2a-3)x+1与x轴交于不同的两点,
∴Δ＞0，即(2a-3)2-4＞0，解得a＜或a＞.
即q:a＜或a＞. 5分
∵p∧q为假，p∨q为真,
∴p真q假或p假q真, 6分
即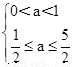
或
9分
解得≤a＜1或a＞. 12分
考点：本题考查了简易逻辑的运用
点评：此类问题解题关键是先确定命题p、q的真假情况，然后再利用真值表作出判断．
练习册系列答案
阅读快车系列答案
相关题目
，0，
，1；b＝－1，0，1|}，平面上点的集合Q＝{(x，y)|x＝－
，0，
，1；y＝－1，0，1|}，则在同一直角坐标系中，P中函数f(x)的图像恰好经过Q中两个点的函数的个数是