Question

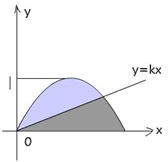
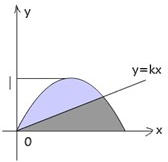如图，直线y=kx将曲线y=-

1

π2

(x-π)2+1(0≤x≤2π)与x轴所围成的图形分成了面积相等的两部分，求k的值．

Answer 1

分析：利用导数的运算法则化为微积分基本定理即可得出．

解答：解：∵

∫

2π 0

(-

1

π2

x2+

2

π

x)dx=-

1

3π2

x3

.

2π 0

+

x2

π

.

2π 0

=

4π

3

，
设曲线y=-

1

π2

x2+

2x

π

与直线y=kx相交与点（t，kt），
∴kt=-

t2

π2

+

2t

π

，即交点为（0，0）或（2π-kπ²，2kπ-k²π²），
∴

∫

t 0

(-

1

π2

x2+

2-kπ

π

x)dx=-

1

3π2

x3

.

t 0

+

2-kπ

2π

x2

.

t 0

=

2-kπ

2π

t2-

1

3π2

t3=

2π

3

把t=2π-kπ²代入上式有：k=

2- 3 4

π

．

点评：熟练掌握导数的运算法则化为微积分基本定理是解题的关键．