Question

以平行六面体相邻两个面上相互异面的两条对角线的端点为顶点的四面体的体积是平行六面体的体积的：（　　）

• A、

  1

  6

• B、

  1

  4

• C、

  1

  3

• D、

  1

  5

Answer 1

分析：以A₁B和B₁C的端点为顶点的四面体是三棱锥A₁-BB₁C，将原平行六面体看作是四棱柱ADD₁A₁-BCC₁B₁，从而找到三棱锥与四棱柱的底面积，高之间的关系，从而得到体积关系．

解答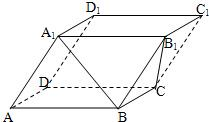：解：如图，以A₁B和B₁C的端点为顶点的四面体是三棱锥A₁-BB₁C，
将原平行六面体视为四棱柱ADD₁A₁-BCC₁B₁，
易见三棱锥的底面积是四棱柱的底面积的一半，高相等，
故三棱锥的体积是四棱柱的体积的

1

6

，
故选A．

点评：本题主要考查平行六面体的结构特征及体积的求法，是常考类型，属基础题．