题目内容
已知三角形ABC的两个顶点A(-1,5)和B(0,-1),又知∠C的平分线所在的直线方程为2x-3y+6=0,求直线AB、BC方程.
【答案】分析:由直线方程的两点式,可求出直线AB的方程,再化成一般式即可.设CD是△ABC中角C的平分线,点B关于CD的对称点为B',可得直线AB'即为直线AC.利用求对称的方法建立方程组,解出B'(-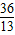 ,
,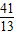 ),结合直线方程的两点式,得出直线AC的方程,联解AC、CD的方程,算出它们的交点C(-
),结合直线方程的两点式,得出直线AC的方程,联解AC、CD的方程,算出它们的交点C(-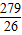 ,-
,-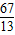 ),由此不难算出直线BC的一般式方程.
),由此不难算出直线BC的一般式方程.
解答:解: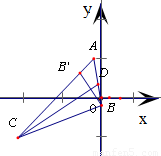 设CD是△ABC中角C的平分线,点B关于CD的对称点为B',
设CD是△ABC中角C的平分线,点B关于CD的对称点为B',
则点B'落在AC所在直线上,直线AB'即为直线AC
设点B'(m,n),可得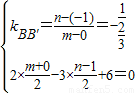
解之得m=-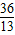 ,n=
,n=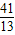 ,可得B'(-
,可得B'(-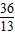 ,
,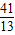 )
)
∴直线AB'方程为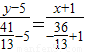 ,化简得24x-23y+139=0
,化简得24x-23y+139=0
即直线AC方程为24x-23y+139=0,由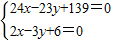 联解得C(-
联解得C(-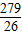 ,-
,-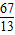 )
)
因此,直线BC的斜率kBC= =
=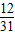 ,可得直线BC方程为y=
,可得直线BC方程为y=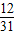 x-1,化成一般式为12x-31y-31=0
x-1,化成一般式为12x-31y-31=0
由直线方程的两点式,得直线AB方程为: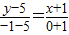 ,整理得6x+y+1=0
,整理得6x+y+1=0
综上所述,得直线AB方程为6x+y+1=0,直线BC方程为12x-31y-31=0.
点评:本题给出三角形的两个顶点坐标和第三个角的平分线方程,求它的两条边所在直线方程,着重考查了直线的相互关系、直线方程的几种形式及其互化等知识,属于基础题.
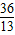 ,
,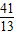 ),结合直线方程的两点式,得出直线AC的方程,联解AC、CD的方程,算出它们的交点C(-
),结合直线方程的两点式,得出直线AC的方程,联解AC、CD的方程,算出它们的交点C(-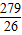 ,-
,-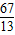 ),由此不难算出直线BC的一般式方程.
),由此不难算出直线BC的一般式方程.解答:解:
 设CD是△ABC中角C的平分线,点B关于CD的对称点为B',
设CD是△ABC中角C的平分线,点B关于CD的对称点为B',则点B'落在AC所在直线上,直线AB'即为直线AC
设点B'(m,n),可得
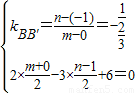
解之得m=-
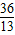 ,n=
,n=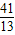 ,可得B'(-
,可得B'(-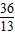 ,
,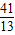 )
)∴直线AB'方程为
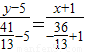 ,化简得24x-23y+139=0
,化简得24x-23y+139=0即直线AC方程为24x-23y+139=0,由
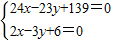 联解得C(-
联解得C(-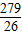 ,-
,-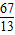 )
)因此,直线BC的斜率kBC=
 =
=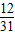 ,可得直线BC方程为y=
,可得直线BC方程为y=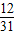 x-1,化成一般式为12x-31y-31=0
x-1,化成一般式为12x-31y-31=0由直线方程的两点式,得直线AB方程为:
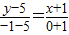 ,整理得6x+y+1=0
,整理得6x+y+1=0综上所述,得直线AB方程为6x+y+1=0,直线BC方程为12x-31y-31=0.
点评:本题给出三角形的两个顶点坐标和第三个角的平分线方程,求它的两条边所在直线方程,着重考查了直线的相互关系、直线方程的几种形式及其互化等知识,属于基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
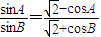 .
.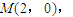 N(1,0),过N的直线与曲线E的交点是D、E.求kDM+kEM的值.
N(1,0),过N的直线与曲线E的交点是D、E.求kDM+kEM的值.