Question

（06年北京卷理）（14分）

在数列中，若是正整数，且，则称为“绝对差数列”.

（Ⅰ）举出一个前五项不为零的“绝对差数列”（只要求写出前十项）；

（Ⅱ）若“绝对差数列”中，，数列满足，，分别判断当时，与的极限是否存在，如果存在，求出其极限值；

（Ⅲ）证明：任何“绝对差数列”中总含有无穷多个为零的项.

Answer 1

解析：（Ⅰ）,（答案不惟一）

（Ⅱ）因为在绝对差数列中,.所以自第 20 项开始，该数列是,,

即自第 20 项开始。每三个相邻的项周期地取值 3，0，3. 所以当时，的极限

不存在.

当时, ,所以
（Ⅲ）证明：根据定义，数列必在有限项后出现零项.证明如下
 假设中没有零项，由于,所以对于任意的n，都有,从而
 当时, ;
 当 时,
 即的值要么比至少小1，要么比至少小1.
令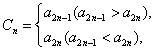
则
由于是确定的正整数，这样减少下去，必然存在某项 ，这与()
矛盾. 从而必有零项.
若第一次出现的零项为第项，记，则自第项开始，每三个相邻的项周期地取值 0，,  , 即

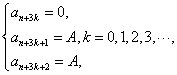
所以绝对差数列中有无穷多个为零的项.