题目内容
以下两题任选一题:(若两题都做,按第一题评分)(1)若圆C的参数方程为
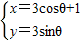 (θ为参数),则圆心的坐标为 ,圆C与直线x+y-3=0的交点个数为 .
(θ为参数),则圆心的坐标为 ,圆C与直线x+y-3=0的交点个数为 .(2)设函数f(x)=|x-a|+3x其中a>0,
(Ⅰ)当a=1时,不等式f(x)≥3x+2的解集为 ;
(II)f(x)≤0的解集为{x|x≤-1},则 a= .
【答案】分析:(1)利用同角三角函数的基本关系消去参数,化为普通方程,求出圆心和半径,再利用点到直线的距离公式求得
圆心到直线的距离,和半径作对比,可得直线和圆的位置关系.
(2)(Ⅰ)当a=1时,不等式即|x-1|+3x≥3x+2,可化为|x-1|≥2,由此求得不等式的解集.
(Ⅱ)由f(x)≤0可得|x-a|+3x≤0,求得解集为{x|x<-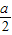 }.再由f(x)≤0的解集为{x|x≤-1},
}.再由f(x)≤0的解集为{x|x≤-1},
故有-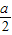 =-1,由此求得a的值.
=-1,由此求得a的值.
解答:解:(1)∵圆C的参数方程为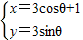 (θ为参数),利用同角三角函数的基本关系消去参数,
(θ为参数),利用同角三角函数的基本关系消去参数,
化为普通方程为 (x-1)2+y2=9,故圆心坐标为(1,0),半径等于3.
圆心到直线x+y-3=0的距离d=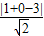 =
=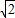 ,小于半径,故直线和圆相交,
,小于半径,故直线和圆相交,
故答案为 (1,0)、2.
(2)(Ⅰ)当a=1时,不等式f(x)≥3x+2即|x-1|+3x≥3x+2,即|x-1|≥2,
∴x-1≥2,或 x-1≤-2.
解得 x≥3,或 x≤-1,故不等式的解集为{x|x≥3,或 x≤-1},
故答案为 {x|x≥3,或 x≤-1}.
(Ⅱ)由f(x)≤0可得|x-a|+3x≤0,∴|x-a|≤-3x,∴3x≤x-a≤-3x.
解得 x<-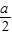 ,故不等式f(x)≤0的解集为{x|x<-
,故不等式f(x)≤0的解集为{x|x<-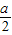 }.
}.
又已知f(x)≤0的解集为{x|x≤-1},故有-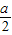 =-1,a=2,
=-1,a=2,
故答案为 2.
点评:本题主要考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,绝对值不等式的解法,属于中档题.
圆心到直线的距离,和半径作对比,可得直线和圆的位置关系.
(2)(Ⅰ)当a=1时,不等式即|x-1|+3x≥3x+2,可化为|x-1|≥2,由此求得不等式的解集.
(Ⅱ)由f(x)≤0可得|x-a|+3x≤0,求得解集为{x|x<-
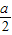 }.再由f(x)≤0的解集为{x|x≤-1},
}.再由f(x)≤0的解集为{x|x≤-1},故有-
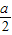 =-1,由此求得a的值.
=-1,由此求得a的值.解答:解:(1)∵圆C的参数方程为
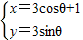 (θ为参数),利用同角三角函数的基本关系消去参数,
(θ为参数),利用同角三角函数的基本关系消去参数,化为普通方程为 (x-1)2+y2=9,故圆心坐标为(1,0),半径等于3.
圆心到直线x+y-3=0的距离d=
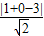 =
=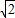 ,小于半径,故直线和圆相交,
,小于半径,故直线和圆相交,故答案为 (1,0)、2.
(2)(Ⅰ)当a=1时,不等式f(x)≥3x+2即|x-1|+3x≥3x+2,即|x-1|≥2,
∴x-1≥2,或 x-1≤-2.
解得 x≥3,或 x≤-1,故不等式的解集为{x|x≥3,或 x≤-1},
故答案为 {x|x≥3,或 x≤-1}.
(Ⅱ)由f(x)≤0可得|x-a|+3x≤0,∴|x-a|≤-3x,∴3x≤x-a≤-3x.
解得 x<-
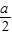 ,故不等式f(x)≤0的解集为{x|x<-
,故不等式f(x)≤0的解集为{x|x<-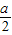 }.
}.又已知f(x)≤0的解集为{x|x≤-1},故有-
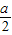 =-1,a=2,
=-1,a=2,故答案为 2.
点评:本题主要考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,绝对值不等式的解法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
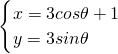 (θ为参数),则圆心的坐标为________,圆C与直线x+y-3=0的交点个数为________.
(θ为参数),则圆心的坐标为________,圆C与直线x+y-3=0的交点个数为________.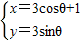 (θ为参数),则圆心的坐标为 ,圆C与直线x+y-3=0的交点个数为 .
(θ为参数),则圆心的坐标为 ,圆C与直线x+y-3=0的交点个数为 .