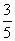题目内容
从有
个红球和个黒球的口袋内任取个球，互斥而不对立的两个事件是：
| A．至少有一个黒球与都是黒球 | B．至少有一个红球与都是红球 |
C．至少有一个黒球与至少有 个红球 | D．恰有个黒球与恰有个黒球 |
D
解析试题分析：对立事件是在互斥的基础之上，在一次试验中两个事件必定有一个要发生．据此，对各选项依次加以分析即可．根据题意，从有个红球和个黒球的口袋内任取个球，选项A，“至少有一个黑球”发生时，“都是黑球”也会发生，故A不互斥，当然不对立；，对于B,至少有一个红球包含都是红球，不是互斥事件，对于C, 至少有一个黒球与至少有个红球,分别都包含一个黑球和一个红球，故不互斥，故选D.
考点：互斥事件与对立事件
点评：本题考查了随机事件当中“互斥”与“对立”的区别与联系，属于基础题．
练习册系列答案
相关题目
已知随机变量
服从正态分布
,若
，则
| A．0.477 | B．0.625 | C．0.954 | D．0.977 |
某产品分甲、乙、丙三级，其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03，丙级品的概率为0.01，则对成品抽查一件抽得正品的概率为( )
| A．0.99 | B．0.98 | C．0.97 | D．0.96 |
的值越大，说明拟合的效果越好；
服从正态分布
，则
；
与
，若它们的随机变量
的观测值
越小，则判断“
